2. Bases du langage R▲
|
Objectifs du chapitre |
|---|
|
Pour utiliser un langage de programmation, il faut en connaître la syntaxe et la sémantique, du moins dans leurs grandes lignes. C'est dans cet esprit que ce chapitre introduit des notions de base du langage R telles que l'expression, l'affectation et l'objet. Le concept de vecteur se trouvant au cœur du langage, le chapitre fait une large place à la création et à la manipulation des vecteurs et autres types d'objets de stockage couramment employés en programmation en R.
|
Énoncé du problème |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Une ligue de hockey compte huit équipes. Le classement de la ligue est disponible quotidiennement dans le journal dans le format habituel ; voir le tableau 2.1.
Tableau 2.1 : Classement de la ligue de hockey pour le problème à résoudre du chapitre. MJ - matchs joués ; V - victoires ; D - défaites ; DP : défaites en prolongation ; PTS - points. Afin d'effectuer différentes analyses statistiques, on désire intégrer ces données dans un espace de travail R. On doit donc déterminer le type d'objet R approprié pour stocker le classement de la ligue. Ensuite, on souhaite extraire les valeurs suivantes de l'objet précédemment créé.
|
2-1. Commandes R▲
Comme vu au chapitre précédent, l'utilisateur de R interagit avec l'interprète R en entrant des commandes à l'invite de commande. Toute commande R est soit une expression, soit une affectation.
-
Normalement, une expression est immédiatement évaluée et le résultat est affiché à l'écran :
Sélectionnez1.
2.
3.
4.
5.
6.>2+3[1]5>pi[1]3.141593>cos(pi/4)[1]0.7071068Dans les anciennes versions de S et R, on pouvait affecter avec le caractère de soulignement « _ ». Cet emploi n'est plus permis, mais la pratique subsiste dans le mode ESS de Emacs. Ainsi, taper le caractère « _ » hors d'une chaîne de caractères dans Emacs génère automatiquement ␣<-␣. Si on souhaite véritablement obtenir le caractère de soulignement, il suffit d'appuyer deux fois successives sur « _ ».
-
Lors d'une affectation, une expression est évaluée, mais le résultat est stocké dans un objet (variable) et rien n'est affiché à l'écran. Le symbole d'affectation est « <- », c'est-à-dire les deux caractères « < » et « - » placés obligatoirement l'un à la suite de l'autre :
Sélectionnez1.
2.
3.
4.
5.
6.>a<-5>a[1]5>b<-a>b[1]5 -
Pour affecter le résultat d'un calcul dans un objet et simultanément afficher ce résultat, il suffit de placer l'affectation entre parenthèses pour ainsi créer une nouvelle expression(4) :
Sélectionnez>(a<-2+3)[1]5 -
Le symbole d'affectation inversé « -> » existe aussi, mais il est rarement utilisé.
-
Éviter d'utiliser l'opérateur « = » pour affecter une valeur à une variable puisque cette pratique est susceptible d'engendrer de la confusion avec les constructions nom = valeur dans les appels de fonction.
Que ce soit dans les fichiers de script ou à la ligne de commande, on sépare les commandes R les unes des autres par un point-virgule « ; » ou par un retour à la ligne.
-
On considère généralement comme du mauvais style d'employer les deux, c'est-à-dire de placer des points-virgules à la fin de chaque ligne de code, surtout dans les fichiers de script.
-
Le point-virgule peut être utile pour séparer deux courtes expressions ou plus sur une même ligne :
Sélectionnez>a<-5; a+2[1]7C'est le seul emploi du point-virgule que l'on rencontrera dans cet ouvrage.
On peut regrouper plusieurs commandes en une seule expression en les entourant d'accolades { }.
-
Le résultat du regroupement est la valeur de la dernière commande :
Sélectionnez1.
2.
3.
4.
5.
6.>{+a<-2+3+b<-a+b+}[1]5 -
Par conséquent, si le regroupement se termine par une assignation, aucune valeur n'est retournée ni affichée à l'écran :
Sélectionnez1.
2.
3.
4.>{+a<-2+3+b<-a+} -
Les règles ci-dessus joueront un rôle important dans la composition de fonctions ; voir le chapitre 5Fonctions définies par l'usager.
- Comme on peut le voir ci-dessus, lorsqu'une commande n'est pas complète à la fin de la ligne, l'invite de commande de R change de >␣ à +␣ pour nous inciter à compléter notre commande.
2-2. Conventions pour les noms d'objets▲
Les caractères permis pour les noms d'objets sont les lettres minuscules a-z et majuscules A-Z, les chiffres 0-9, le point « . » et le caractère de soulignement « _ ». Selon l'environnement linguistique de l'ordinateur, il peut être permis d'utiliser des lettres accentuées, mais cette pratique est fortement découragée puisqu'elle risque de nuire à la portabilité du code.
- Les noms d'objets ne peuvent commencer par un chiffre. S'ils commencent par un point, le second caractère ne peut être un chiffre.
- Le R est sensible à la casse, ce qui signifie que foo, Foo et FOO sont trois objets distincts. Un moyen simple d'éviter des erreurs liées à la casse consiste à n'employer que des lettres minuscules.
-
Certains noms sont utilisés par le système R, aussi vaut-il mieux éviter de les utiliser. En particulier, éviter d'utiliser
Sélectionnezc,q,t,C,D,I,diff,length,mean,pi,range,var -
Certains mots sont réservés et il est interdit de les utiliser comme nom d'objet. Les mots réservés pour le système sont :
Sélectionnez1.
2.
3.
4.
5.break,else,for,function,if,in,next,repeat,return,while,TRUE,FALSE,Inf,NA,NaN,NULL, NA_integer_, NA_real_, NA_complex_, NA_character_, ... , ..1, ..2, etc.Oui, ... (point-point-point) est véritablement un nom d'objet dans R ! Son usage est expliqué à la section 6.1Argument '...'.
-
Les variables T et F prennent par défaut les valeurs
TRUEetFALSE, respectivement, mais peuvent être réaffectées :Sélectionnez1.
2.
3.
4.
5.
6.
7.
8.
9.>T[1]TRUE>F[1]FALSE>TRUE<-3ErrorinTRUE<-3:membre gauchedel′assignation (do_set) incorrect>(T<-3)[1]3 - Nous recommandons de toujours écrire les valeurs booléennes
TRUEetFALSEau long pour éviter des bogues difficiles à détecter.
2-3. Les objets R▲
Tout dans le langage R est un objet : les variables contenant des données, les fonctions, les opérateurs, même le symbole représentant le nom d'un objet est lui-même un objet. Les objets possèdent au minimum un mode et une longueur et certains peuvent être dotés d'un ou plusieurs attributs.
- Le mode d'un objet est obtenu avec la fonction mode :
> v <- c(1, 2, 5, 9)
> mode(v)
[1] "numeric"- La longueur d'un objet est obtenue avec la fonction length :
> length(v)
[1] 42-3-1. Modes et types de données▲
Le mode prescrit ce qu'un objet peut contenir. À ce titre, un objet ne peut avoir qu'un seul mode. Le tableau 2.2 contient la liste des principaux modes disponibles en R. À chacun de ces modes correspond une fonction du même nom servant à créer un objet de ce mode.
- Les objets de mode « numeric », « complex », « logical » et « character » sont des objets simples (atomic en anglais) qui ne peuvent contenir que des données d'un seul type.
- En revanche, les objets de mode « list » ou « expression » sont des objets récursifs qui peuvent contenir d'autres objets. Par exemple, une liste peut contenir une ou plusieurs autres listes ; voir la section 2.6Listes pour plus de détails.
- La fonction typeof permet d'obtenir une description plus précise de la représentation interne d'un objet (c'est-à-dire au niveau de la mise en œuvre en C). Le mode et le type d'un objet sont souvent identiques.
2-3-2. Longueur▲
La longueur d'un objet est égale au nombre d'éléments qu'il contient.
-
La longueur, au sens R du terme, d'une chaîne de caractères est toujours 1. Un objet de mode character doit contenir plusieurs chaînes de caractères pour que sa longueur soit supérieure à 1 :
Sélectionnez1.
2.
3.
4.
5.
6.>v1<-"actuariat">length(v1)[1]1>v2<-c("a","c","t","u","a","r","i","a","t")>length(v2)[1]9 -
Il faut utiliser la fonction nchar pour obtenir le nombre de caractères dans une chaîne :
Sélectionnez1.
2.
3.
4.>nchar(v1)[1]9>nchar(v2)[1]111111111 - Un objet peut être de longueur 0 et doit alors être interprété comme un contenant qui existe, mais qui est vide :
2.
3.
> v <- numeric(0)
> length(v)
[1] 0
2-3-3. Objet spécial NULL▲
L'objet spécial NULL représente « rien », ou le vide.
2-3-4. Valeurs manquantes, indéterminées et infinies▲
Dans les applications statistiques, il est souvent utile de pouvoir représenter des données manquantes. Dans R, l'objet spécial NA remplit ce rôle.
- Par défaut, le mode de
NAest logical, maisNAne peut être considéré ni commeTRUE, ni commeFALSE. - Toute opération impliquant une donnée
NAa comme résultatNA. - Certaines fonctions (sum, mean, par exemple) ont par conséquent un argument na.rm qui, lorsque
TRUE, élimine les données manquantes avant de faire un calcul. -
La valeur
NAn'est égale à aucune autre, pas même elle-même (selon la règle ci-dessus, le résultat de la comparaison estNA) :Sélectionnez>NA==NA[1]NA - Par conséquent, pour tester si les éléments d'un objet sont NA ou non il faut utiliser la fonction is.na :
> is.na(NA)
[1] TRUELa norme IEEE 754 régissant la représentation interne des nombres dans un ordinateur (IEEE, 2003) prévoit les valeurs mathématiques spéciales +∞ et −∞ ainsi que les formes indéterminées du type kitxmlcodeinlinelatexdvp\frac{0}{0}finkitxmlcodeinlinelatexdvp ou kitxmlcodeinlinelatexdvp\infty - \inftyfinkitxmlcodeinlinelatexdvp. R dispose d'objets spéciaux pour représenter ces valeurs.
2-3-5. Attributs▲
Les attributs d'un objet sont des éléments d'information additionnels liés à cet objet. La liste des attributs les plus fréquemment rencontrés se trouve au tableau 2.3. Pour chaque attribut, il existe une fonction du même nom servant à extraire l'attribut correspondant d'un objet.
- Plus généralement, la fonction attributes permet d'extraire ou de modifier la liste des attributs d'un objet. On peut aussi travailler sur un seul attribut à la fois avec la fonction attr.
-
On peut ajouter à peu près ce que l'on veut à la liste des attributs d'un objet. Par exemple, on pourrait vouloir attacher au résultat d'un calcul la méthode de calcul utilisée :
Sélectionnez1.
2.
3.
4.
5.>x<-3>attr(x,"methode")<-"au pif">attributes(x)$methode[1]"au pif" -
Extraire un attribut qui n'existe pas retourne
NULL:Sélectionnez>dim(x)NULL - À l'inverse, donner à un attribut la valeur
NULLefface cet attribut :
2.
3.
> attr(x, "methode") <- NULL
> attributes(x)
NULL
2-4. Vecteurs▲
En R, à toutes fins pratiques, tout est un vecteur. Contrairement à certains autres langages de programmation, il n'y a pas de notion de scalaire en R ; un scalaire est simplement un vecteur de longueur 1. Comme nous le verrons au chapitre 3Opérateurs et fonctions, le vecteur est l'unité de base dans les calculs.
- Dans un vecteur simple, tous les éléments doivent être du même mode. Nous nous restreignons à ce type de vecteurs pour le moment.
-
Les fonctions de base pour créer des vecteurs sont :
-
Il est possible (et souvent souhaitable) de donner une étiquette à chacun des éléments d'un vecteur.
Sélectionnez1.
2.
3.
4.
5.
6.
7.
8.>(v<-c(a=1, b=2,c=5)) a bc125>v<-c(1,2,5)>names(v)<-c("a","b","c")>v a bc125Ces étiquettes font alors partie des attributs du vecteur.
- L'indiçage dans un vecteur se fait avec les crochets [ ]. On peut extraire un élément d'un vecteur par sa position ou par son étiquette, si elle existe (auquel cas cette approche est beaucoup plus sûre).
2.
3.
4.
> v[3]
c5
> v["c"]
c5
La section 2.8Indiçage traite plus en détail de l'indiçage des vecteurs et des matrices.
Dans un vecteur simple, tous les éléments doivent être du même mode. Or, les informations du classement de la ligue comportent à la fois des chaînes de caractères et des nombres. De plus, le classement se présente sous forme d'un tableau à deux dimensions, alors qu'un vecteur n'en compte qu'une seule. Le vecteur simple n'est donc pas le type d'objet approprié pour stocker le classement de la ligue.
2-5. Matrices et tableaux▲
Le R étant un langage spécialisé pour les calculs mathématiques, il supporte tout naturellement et de manière intuitive — à une exception près, comme nous le verrons — les matrices et, plus généralement, les tableaux à plusieurs dimensions.
Les ![]() matrices et tableaux ne sont rien d'autre que des vecteurs dotés d'un attribut dim. Ces objets sont donc stockés, et peuvent être manipulés, exactement comme des vecteurs simples.
matrices et tableaux ne sont rien d'autre que des vecteurs dotés d'un attribut dim. Ces objets sont donc stockés, et peuvent être manipulés, exactement comme des vecteurs simples.
- Une matrice est un vecteur avec un attribut dim de longueur 2. Cela change implicitement la classe de l'objet pour « matrix » et, de ce fait, le mode d'affichage de l'objet ainsi que son interaction avec plusieurs opérateurs et fonctions.
-
La fonction de base pour créer des matrices est matrix :
Sélectionnez1.
2.
3.
4.
5.
6.
7.
8.>matrix(1:6,nrow=2,ncol=3)[,1][,2][,3][1,]135[2,]246>matrix(1:6,nrow=2,ncol=3, byrow=TRUE)[,1][,2][,3][1,]123[2,]456 -
La généralisation d'une matrice à plus de deux dimensions est un tableau (array). Le nombre de dimensions du tableau est toujours égal à la longueur de l'attribut dim. La classe implicite d'un tableau est « array ».
- La fonction de base pour créer des tableaux est array :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
> array(1:24, dim = c(3, 4, 2))
, , 1
[,1] [,2] [,3] [,4]
[1,] 1 4 7 10
[2,] 2 5 8 11
[3,] 3 6 9 12
, , 2
[,1] [,2] [,3] [,4]
[1,] 13 16 19 22
[2,] 14 17 20 23
[3,] 15 18 21 24
On remarquera ci-dessus que les matrices et tableaux sont remplis en faisant d'abord varier la première dimension, puis la seconde, etc. Pour les matrices, cela revient à remplir par colonne. On conviendra que cette convention, héritée du Fortran, n'est pas des plus intuitives.
La fonction matrix a un argument byrow qui permet d'inverser l'ordre de remplissage. Cependant, il vaut mieux s'habituer à la convention de R que d'essayer constamment de la contourner.
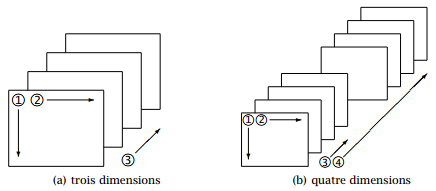
L'ordre de remplissage inhabituel des tableaux rend leur manipulation difficile si on ne les visualise pas correctement. Imaginons un tableau de dimensions 3 × 4 × 5.
- Il faut voir le tableau comme cinq matrices 3 × 4 (remplies par colonne !) les unes derrière les autres.
- Autrement dit, le tableau est un prisme rectangulaire haut de 3 unités, large de 4 et profond de 5.
- Si l'on ajoute une quatrième dimension, cela revient à aligner des prismes les uns derrière les autres, et ainsi de suite.
La figure 2.1 fournit une représentation schématique des tableaux à trois et quatre dimensions.
Comme pour les vecteurs, l'indiçage des matrices et tableaux se fait avec les crochets [ ].
-
On extrait un élément d'une matrice en précisant sa position dans chaque dimension de celle-ci, séparées par des virgules :
Sélectionnez1.
2.
3.
4.
5.
6.
7.>(m<-matrix(c(40,80,45,21,55,32),+nrow=2,ncol=3))[,1][,2][,3][1,]404555[2,]802132>m[1,2][1]45 -
On peut aussi ne donner que la position de l'élément dans le vecteur sous-jacent :
Sélectionnez>m[3][1]45 -
Lorsqu'une dimension est omise dans les crochets, tous les éléments de cette dimension sont extraits :
Sélectionnez>m[2,][1]802132 -
Les idées sont les mêmes pour les tableaux.
- Pour le reste, les règles d'indiçage de vecteurs exposées à la section 2.8Indiçage s'appliquent à chaque position de l'indice d'une matrice ou d'un tableau.
Des fonctions permettent de fusionner des matrices et des tableaux ayant au moins une dimension identique.
- La fonction rbind permet de fusionner verticalement deux matrices (ou plus) ayant le même nombre de colonnes.
2.
3.
4.
5.
6.
7.
8.
> n <- matrix(1:9, nrow = 3)
> rbind(m, n)
[,1] [,2] [,3]
[1,] 40 45 55
[2,] 80 21 32
[3,] 1 4 7
[4,] 2 5 8
[5,] 3 6 9
- La fonction cbind permet de fusionner horizontalement deux matrices (ou plus) ayant le même nombre de lignes.
2.
3.
4.
5.
> n <- matrix(1:4, nrow = 2)
> cbind(m, n)
[,1] [,2] [,3] [,4] [,5]
[1,] 40 45 55 1 3
[2,] 80 21 32 2 4
Une matrice convient bien pour stocker un tableau de données. Toutefois, puisque la matrice est en fait un vecteur avec un attribut dim de longueur 2, tous les éléments doivent être du même mode, comme c'était le cas avec les vecteurs simples. Impossible dans ce cas d'y stocker le nom des équipes. La matrice n'est toujours pas le type d'objet approprié.
2-6. Listes▲
La liste est le mode de stockage le plus général et polyvalent du langage R. Il s'agit d'un type de vecteur spécial dont les éléments peuvent être de n'importe quel mode, y compris le mode list. Cela permet donc d'emboîter des listes, d'où le qualificatif de récursif pour ce type d'objet.
-
La fonction de base pour créer des listes est list :
Sélectionnez1.
2.
3.
4.
5.
6.
7.>(x<-list(size=c(1,5,2), user="Joe",new=TRUE))$size[1]152$user[1]"Joe"$new[1]TRUECi-dessus, le premier élément de la liste est de mode « numeric », le second de mode « character » et le troisième de mode « logical ».
-
Nous recommandons de nommer les éléments d'une liste. En effet, les listes contiennent souvent des données de types différents et il peut s'avérer difficile d'identifier les éléments s'ils ne sont pas nommés. De plus, comme nous le verrons ci-dessous, il est très simple d'extraire les éléments d'une liste par leur étiquette.
-
La liste demeure un vecteur. On peut donc l'indicer avec l'opérateur [ ]. Cependant, cela retourne une liste contenant le ou les éléments indicés. C'est rarement ce que l'on souhaite.
-
Pour indicer un élément d'une liste et n'obtenir que cet élément, et non une liste contenant l'élément, il faut utiliser l'opérateur d'indiçage [[ ]].
Comparer
Sélectionnez>x[1]$size[1]152et
Sélectionnez>x[[1]][1]152Évidemment, on ne peut extraire qu'un seul élément à la fois avec les crochets doubles [[ ]] .
-
Petite subtilité peu employée, mais élégante. Si l'indice utilisé dans [[ ]] est un vecteur, il est utilisé récursivement pour indicer la liste : cela sélectionnera la composante de la liste correspondant au premier élément du vecteur, puis l'élément de la composante correspondant au second élément du vecteur, et ainsi de suite.
-
Une autre — la meilleure, en fait — façon d'indicer un seul élément d'une liste est par son étiquette avec l'opérateur $ :
Sélectionnez>x$size[1]152 - La fonction unlist convertit une liste en un vecteur simple. Elle est surtout utile pour concaténer les éléments d'une liste lorsque ceux-ci sont des scalaires. Attention, cette fonction peut être destructrice si la structure interne de la liste est importante.
2-7. Data frames▲
Les vecteurs, les matrices, les tableaux et les listes sont les types d'objets les plus fréquemment utilisés en programmation en R. Toutefois, un grand nombre de procédures statistiques — pensons à la régression linéaire, par exemple — reposent davantage sur les data frames pour le stockage des données.
- Un est une liste de classe « data.frame » dont tous les éléments sont de la même longueur (ou comptent le même nombre de lignes si les éléments sont des matrices).
- Il est généralement représenté sous la forme d'un tableau à deux dimensions. Chaque élément de la liste sous-jacente correspond à une colonne.
- Bien que visuellement similaire à une matrice un data frame est plus général puisque les colonnes peuvent être de modes différents ; pensons à un tableau avec des noms (mode character) dans une colonne et des notes (mode numeric) dans une autre.
- On crée un data frame avec la fonction data.frame ou, pour convertir un autre type d'objet en data frame, avec as.data.frame.
- Le data frame peut être indicé à la fois comme une liste et comme une matrice.
- Les fonctions rbind et cbind peuvent être utilisées pour ajouter des lignes ou des colonnes à un data frame.
- On peut rendre les colonnes d'un data frame (ou d'une liste) visibles dans l'espace de travail avec la fonction attach, puis les masquer avec detach.
La liste permettrait de stocker à la fois le nom des équipes et leurs statistiques puisqu'elle peut contenir des objets de modes différents.
On crée d'abord des vecteurs simples contenant les données de chaque colonne du classement des équipes.
2.
3.
4.
5.
6.
7.
8.
> Equipe <- c("Washington", "Dallas", "Chicago",
+ "Los Angeles", "St-Louis", "Détroit",
+ "Montréal", "Boston")
> MJ <- c(55, 56, 57, 58, 56, 57, 56, 57)
> V <- c(36, 32, 30, 30, 25, 25, 22, 24)
> D <- c(16, 19, 21, 22, 19, 21, 27, 31)
> DP <- c( 3, 5, 6, 6, 12, 11, 7, 2)
> PTS <- c(75, 69, 66, 66, 62, 61, 51, 50)
On les combine ensuite sous forme de liste nommée.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
> list(Equipe = Equipe, MJ = MJ, V = V, D = D,
+ DP = DP, PTS = PTS)
$Equipe
[1] "Washington" "Dallas" "Chicago"
[4] "Los Angeles" "St-Louis" "Détroit"
[7] "Montréal" "Boston"
$MJ
[1] 55 56 57 58 56 57 56 57
$V
[1] 36 32 30 30 25 25 22 24
$D
[1] 16 19 21 22 19 21 27 31
$DP
[1] 3 5 6 6 12 11 7 2
$PTS
[1] 75 69 66 66 62 61 51 50
On constate que R ne présente pas le contenu de la liste sous forme d'un tableau. Ce n'est donc pas le type d'objet le mieux approprié pour stocker un classement. En fait, la liste est un mode de stockage trop général pour le type de données dont nous disposons.
L'élément distinctif entre un data frame et une liste générale, c'est que tous les éléments du premier doivent être de la même longueur et que, par conséquent, R les dispose en colonnes. Nous avons donc ici le type d'objet tout désigné pour stocker des données de modes différents, mais qui se présentent sous forme de tableau à deux dimensions.
2-8. Indiçage▲
L'indiçage des vecteurs et matrices a déjà été brièvement présenté aux sections 2.4Vecteurs et 2.5Matrices et tableaux. La présente section contient plus de détails sur cette procédure des plus communes lors de l'utilisation du langage R. On se concentre toutefois sur le traitement des vecteurs.
- L'indiçage sert principalement à deux choses : soit extraire des éléments d'un objet avec la construction x[i], ou les remplacer avec la construction x[i] <- y.
- Il est utile de savoir que ces opérations sont en fait traduites par l'interprète R en des appels à des fonctions nommées [ et [<-, dans l'ordre.
- De même, les opérations d'extraction et de remplacement d'un élément d'une liste de la forme x
$etiquette et x$etiquette<-y correspondent à des appels aux fonctions$et$<-.
Il existe cinq façons d'indicer un vecteur dans le langage R. Dans tous les cas, l'indiçage se fait à l'intérieur de crochets [ ].
-
Avec un vecteur d'entiers positifs. Les éléments se trouvant aux positions correspondant aux entiers sont extraits du vecteur, dans l'ordre. C'est la technique la plus courante :
Sélectionnez1.
2.
3.
4.>x<-c(A=2, B=4,C=-1,D=-5, E=8)>x[c(1,3)]AC2-1 -
Avec un vecteur d'entiers négatifs. Les éléments se trouvant aux positions correspondant aux entiers négatifs sont alors éliminés du vecteur :
Sélectionnez1.
2.
3.>x[c(-2,-3)]ADE2-58 -
Avec un vecteur booléen. Le vecteur d'indiçage doit alors être de la même longueur que le vecteur indicé. Les éléments correspondant à une valeur
TRUEsont extraits du vecteur, alors que ceux correspondant àFALSEsont éliminés :Sélectionnez1.
2.
3.
4.
5.
6.>x>0A BCDETRUETRUEFALSEFALSETRUE>x[x>0]A B E248 -
Avec un vecteur de chaînes de caractères. Utile pour extraire les éléments d'un vecteur à condition que ceux-ci soient nommés :
Sélectionnez1.
2.
3.>x[c("B","D")]BD4-5 - L'indice est laissé vide. Tous les éléments du vecteur sont alors sélectionnés :
2.
3.
> x[]
A B C D E
2 4 -1 -5 8
Cette méthode est essentiellement utilisée avec les matrices et tableaux pour sélectionner tous les éléments d'une dimension (voir l'exemple). Laisser l'indice vide est différent d'indicer avec un vecteur vide ; cette dernière opération retourne un vecteur vide.
|
Solution du problème |
|
Nous avons déjà créé dans cette astuce des vecteurs contenant les données des différentes colonnes du classement de la ligue. Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. On crée l'objet classement qui contiendra le classement de la ligue avec la fonction data.frame. Celle-ci prend en arguments les différents vecteurs de données. Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. On répond ensuite aux questions de traitement des données.
Sélectionnez 1. 2. 3. |
2-9. Exemples▲
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
141.
142.
143.
144.
145.
146.
147.
148.
149.
150.
151.
152.
153.
154.
155.
156.
157.
158.
159.
160.
161.
162.
163.
164.
165.
166.
167.
168.
169.
170.
171.
172.
173.
174.
175.
176.
177.
178.
179.
180.
181.
182.
183.
184.
185.
186.
187.
188.
189.
190.
191.
192.
193.
194.
195.
196.
197.
198.
199.
200.
201.
202.
203.
204.
205.
206.
207.
208.
209.
210.
211.
212.
213.
214.
215.
216.
217.
218.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241.
242.
243.
244.
245.
246.
247.
248.
249.
250.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261.
262.
263.
264.
265.
266.
267.
268.
269.
270.
271.
272.
273.
274.
275.
276.
277.
278.
279.
280.
281.
282.
283.
284.
285.
286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
298.
299.
300.
301.
302.
303.
304.
305.
306.
307.
308.
309.
310.
311.
312.
313.
314.
315.
316.
317.
318.
319.
320.
321.
322.
323.
324.
325.
326.
327.
328.
329.
330.
331.
332.
333.
334.
335.
336.
337.
338.
339.
340.
341.
342.
343.
344.
345.
346.
347.
348.
349.
350.
351.
352.
353.
354.
355.
356.
357.
358.
359.
360.
361.
362.
363.
364.
365.
366.
367.
368.
369.
370.
371.
372.
373.
374.
375.
376.
377.
378.
379.
380.
381.
382.
383.
384.
385.
386.
387.
388.
389.
390.
391.
392.
393.
394.
395.
396.
397.
398.
399.
400.
401.
402.
403.
404.
405.
406.
407.
408.
409.
410.
411.
412.
413.
414.
415.
416.
417.
418.
419.
420.
421.
422.
423.
424.
425.
426.
427.
428.
429.
430.
431.
432.
433.
434.
435.
436.
437.
438.
439.
440.
441.
442.
443.
444.
445.
446.
447.
448.
449.
450.
451.
452.
453.
454.
455.
456.
457.
458.
459.
460.
461.
462.
463.
464.
465.
466.
467.
468.
469.
470.
471.
472.
473.
474.
475.
476.
477.
478.
479.
480.
481.
###
### COMMANDES R
###
## Les expressions entrées à la ligne de commande sont
## immédiatement évaluées et le résultat est affiché à
## l'écran, comme avec une grosse calculatrice.
1 # une constante
(2 + 3 * 5)/7 # priorité des opérations
3^5 # puissance
exp(3) # fonction exponentielle
sin(pi/2) + cos(pi/2) # fonctions trigonométriques
gamma(5) # fonction gamma
## Lorsqu'une expression est syntaxiquement incomplète,
## l'invite de commande change de '> ' à '+ '.
2 - # expression incomplète
5 * # toujours incomplète
3 # complétée
## Taper le nom d'un objet affiche son contenu. Pour une
## fonction, c'est son code source qui est affiché.
pi # constante numérique intégrée
letters # chaîne de caractères intégrée
LETTERS # version en majuscules
matrix # fonction
## Ne pas utiliser '=' pour l'affectation. Les opérateurs
## d'affectation standard en R sont '<-' et '->'.
x <- 5 # affecter 5 à l'objet 'x'
5 -> x # idem, mais peu usité
x # voir le contenu
(x <- 5) # affecter et afficher
y <- x # affecter la valeur de 'x' à 'y'
x <- y <- 5 # idem, en une seule expression
y # 5
x <- 0 # changer la valeur de 'x'...
y # ... ne change pas celle de 'y'
## Pour regrouper plusieurs expressions en une seule commande,
## il faut soit les séparer par un point-virgule ';', soit les
## regrouper à l'intérieur d'accolades { } et les séparer par
## des retours à la ligne.
x <- 5; y <- 2; x + y # compact; éviter dans les scripts
x <- 5; # éviter les ';' superflus
{ # début d'un groupe
x <- 5 # première expression du groupe
y <- 2 # seconde expression du groupe
x + y # résultat du groupe
} # fin du groupe et résultat
{x <- 5; y <- 2; x + y} # valide, mais redondant
###
### NOMS D'OBJETS
###
## Quelques exemples de noms valides et invalides.
foo <- 5 # valide
foo.123 <- 5 # valide
foo_123 <- 5 # valide
123foo <- 5 # invalide; commence par un chiffre
.foo <- 5 # valide
.123foo <- 5 # invalide; point suivi d'un chiffre
## Liste des objets dans l'espace de travail. Les objets dont
## le nom commence par un point sont considérés cachés.
ls() # l'objet '.foo' n'est pas affiché
ls(all.names = TRUE) # objets cachés aussi affichés
## R est sensible à la casse
foo <- 1
Foo
FOO
###
### LES OBJETS R
###
## MODES ET TYPES DE DONNÉES
## Le mode d'un objet détermine ce qu'il peut contenir. Les
## vecteurs simples ("atomic") contiennent des données d'un
## seul type.
mode(c(1, 4.1, pi)) # nombres réels
mode(c(2, 1 + 5i)) # nombres complexes
mode(c(TRUE, FALSE, TRUE)) # valeurs booléennes
mode("foobar") # chaînes de caractères
## Si l'on mélange dans un même vecteur des objets de modes
## différents, il y a conversion automatique vers le mode pour
## lequel il y a le moins de perte d'information, c'est-à-dire
## vers le mode qui permet le mieux de retrouver la valeur
## originale des éléments.
c(5, TRUE, FALSE) # conversion en mode 'numeric'
c(5, "z") # conversion en mode 'character'
c(TRUE, "z") # conversion en mode 'character'
c(5, TRUE, "z") # conversion en mode 'character'
## La plupart des autres types d'objets sont récursifs. Voici
## quelques autres modes.
mode(seq) # une fonction
mode(list(5, "foo", TRUE)) # une liste
mode(expression(x <- 5)) # une expression non évaluée
## LONGUEUR
## La longueur d'un vecteur est égale au nombre d'éléments
## dans le vecteur.
(x <- 1:4)
length(x)
## Une chaîne de caractères ne compte que pour un seul
## élément.
(x <- "foobar")
length(x)
## Pour obtenir la longueur de la chaîne, il faut utiliser
## nchar().
nchar(x)
## Un objet peut néanmoins contenir plusieurs chaînes de
## caractères.
(x <- c("f", "o", "o", "b", "a", "r"))
length(x)
## La longueur peut être 0, auquel cas on a un objet vide,
## mais qui existe.
(x <- numeric(0)) # création du contenant
length(x) # l'objet 'x' existe...
x[1] <- 1 # possible, 'x' existe
X[1] <- 1 # impossible, 'X' n'existe pas
## L'OBJET SPECIAL 'NULL'
mode(NULL) # le mode de 'NULL' est NULL
length(NULL) # longueur nulle
x <- c(NULL, NULL) # s'utilise comme un objet normal
x; length(x); mode(x) # mais donne toujours le vide
## L'OBJET SPÉCIAL 'NA'
x <- c(65, NA, 72, 88) # traité comme une valeur
x + 2 # tout calcul avec 'NA' donne NA
mean(x) # voilà qui est pire
mean(x, na.rm = TRUE) # éliminer les 'NA' avant le calcul
is.na(x) # tester si les données sont 'NA'
## VALEURS INFINIES ET INDÉTERMINÉES
1/0 # +infini
-1/0 # -infini
0/0 # indétermination
x <- c(65, Inf, NaN, 88) # s'utilisent comme des valeurs
is.finite(x) # quels sont les nombres réels ?
is.nan(x) # lesquels ne sont « pas un nombre » ?
## ATTRIBUTS
## Les objets peuvent être dotés d'un ou plusieurs attributs.
data(cars) # jeu de données intégré
attributes(cars) # liste de tous les attributs
attr(cars, "class") # extraction d'un seul attribut
## Attribut 'class'. Selon la classe d'un objet, certaines
## fonctions (dites « fonctions génériques ») vont se comporter
## différemment.
x <- sample(1:100, 10) # échantillon aléatoire de 10
# nombres entre 1 et 100
class(x) # classe de l'objet
plot(x) # graphique pour cette classe
class(x) <- "ts" # 'x' est maintenant une série
# chronologique
plot(x) # graphique pour les séries
# chronologiques
class(x) <- NULL; x # suppression de l'attribut 'class'
## Attribut 'dim'. Si l'attribut 'dim' compte deux valeurs,
## l'objet est traité comme une matrice. S'il en compte plus
## de deux, l'objet est traité comme un tableau (array).
x <- 1:24 # un vecteur
dim(x) <- c(4, 6) # ajoute un attribut 'dim'
x # l'objet est une matrice
dim(x) <- c(4, 2, 3) # change les dimensions
x # l'objet est maintenant un tableau
## Attribut 'dimnames'. Permet d'assigner des étiquettes (ou
## noms) aux dimensions d'une matrice ou d'un tableau.
dimnames(x) <- list(1:4, c("a", "b"), c("A", "B", "C"))
dimnames(x) # remarquer la conversion
x # affichage avec étiquettes
attributes(x) # tous les attributs de 'x'
attributes(x) <- NULL; x # supprimer les attributs
## Attributs 'names'. Similaire à 'dimnames', mais pour les
## éléments d'un vecteur ou d'une liste.
names(x) <- letters[1:24] # attribution d'étiquettes
x # identification facilitée
###
### VECTEURS
###
## La fonction de base pour créer des vecteurs est 'c'. Il
## peut s'avérer utile de donner des étiquettes aux éléments
## d'un vecteur.
x <- c(a = -1, b = 2, c = 8, d = 10) # création d'un vecteur
names(x) # extraire les étiquettes
names(x) <- letters[1:length(x)] # changer les étiquettes
x[1] # extraction par position
x["c"] # extraction par étiquette
x[-2] # élimination d'un élément
## La fonction 'vector' sert à initialiser des vecteurs avec
## des valeurs prédéterminées. Elle compte deux arguments : le
## mode du vecteur et sa longueur. Les fonctions 'numeric',
## 'logical', 'complex' et 'character' constituent des
## raccourcis pour des appels à 'vector'.
vector("numeric", 5) # vecteur initialisé avec des 0
numeric(5) # équivalent
numeric # en effet, voici la fonction
logical(5) # initialisé avec FALSE
complex(5) # initialisé avec 0 + 0i
character(5) # initialisé avec chaînes vides
###
### MATRICES ET TABLEAUX
###
## Une matrice est un vecteur avec un attribut 'dim' de
## longueur 2 une classe implicite "matrix". La manière
## naturelle de créer une matrice est avec la fonction
## 'matrix'.
(x <- matrix(1:12, nrow = 3, ncol = 4)) # créer la matrice
length(x) # 'x' est un vecteur...
dim(x) # ... avec un attribut 'dim'...
class(x) # ... et classe implicite "matrix"
## Une manière moins naturelle mais équivalente --- et parfois
## plus pratique --- de créer une matrice consiste à ajouter
## un attribut 'dim' à un vecteur.
x <- 1:12 # vecteur simple
dim(x) <- c(3, 4) # ajout d'un attribut 'dim'
x; class(x) # 'x' est une matrice!
## Les matrices sont remplies par colonne par défaut. Utiliser
## l'option 'byrow' pour remplir par ligne.
matrix(1:12, nrow = 3, byrow = TRUE)
## Indicer la matrice ou le vecteur sous-jacent est
## équivalent. Utiliser l'approche la plus simple selon le
## contexte.
x[1, 3] # l'élément en position (1, 3)...
x[7] # ... est le 7e élément du vecteur
x[1, ] # première ligne
x[, 2] # deuxième colonne
nrow(x) # nombre de lignes
dim(x)[1] # idem
ncol(x) # nombre de colonnes
dim(x)[2] # idem
## Fusion de matrices et vecteurs.
x <- matrix(1:12, 3, 4) # 'x' est une matrice 3 x 4
y <- matrix(1:8, 2, 4) # 'y' est une matrice 2 x 4
z <- matrix(1:6, 3, 2) # 'z' est une matrice 3 x 2
rbind(x, 1:4) # ajout d'une ligne à 'x'
rbind(x, y) # fusion verticale de 'x' et 'y'
cbind(x, 1:3) # ajout d'une colonne à 'x'
cbind(x, z) # concaténation de 'x' et 'z'
rbind(x, z) # dimensions incompatibles
cbind(x, y) # dimensions incompatibles
## Les vecteurs ligne et colonne sont rarement nécessaires. On
## peut les créer avec les fonctions 'rbind' et 'cbind',
## respectivement.
rbind(1:3) # un vecteur ligne
cbind(1:3) # un vecteur colonne
## Un tableau (array) est un vecteur avec un attribut 'dim' de
## longueur supérieure à 2 et une classe implicite "array".
## Quant au reste, la manipulation des tableaux est en tous
## points identique à celle des matrices. Ne pas oublier:
## les tableaux sont remplis de la première dimension à la
## dernière!
x <- array(1:60, 3:5) # tableau 3 x 4 x 5
length(x) # 'x' est un vecteur...
dim(x) # ... avec un attribut 'dim'...
class(x) # ... une classe implicite "array"
x[1, 3, 2] # l'élément en position (1, 3, 2)...
x[19] # ... est l'élément 19 du vecteur
## Le tableau ci-dessus est un prisme rectangulaire 3 unités
## de haut, 4 de large et 5 de profond. Indicer ce prisme avec
## un seul indice équivaut à en extraire des « tranches », alors
## qu'utiliser deux indices équivaut à en tirer des « carottes »
## (au sens géologique du terme). Il est laissé en exercice de
## généraliser à plus de dimensions...
x # les cinq matrices
x[, , 1] # tranches de haut en bas
x[, 1, ] # tranches d'avant à l'arrière
x[1, , ] # tranches de gauche à droite
x[, 1, 1] # carotte de haut en bas
x[1, 1, ] # carotte d'avant à l'arrière
x[1, , 1] # carotte de gauche à droite
###
### LISTES
###
## La liste est l'objet le plus général en R. C'est un objet
## récursif qui peut contenir des objets de n'importe quel
## mode et longueur.
(x <- list(joueur = c("V", "C", "C", "M", "A"),
score = c(10, 12, 11, 8, 15),
expert = c(FALSE, TRUE, FALSE, TRUE, TRUE),
niveau = 2))
is.vector(x) # vecteur...
length(x) # ... de quatre éléments...
mode(x) # ... de mode "list"
is.recursive(x) # objet récursif
## Comme tout autre vecteur, une liste peut être concaténée
## avec un autre vecteur avec la fonction 'c'.
y <- list(TRUE, 1:5) # liste de deux éléments
c(x, y) # liste de six éléments
## Pour initialiser une liste d'une longueur déterminée, mais
## dont chaque élément est vide, utiliser la fonction
## 'vector'.
vector("list", 5) # liste de NULL
## Pour extraire un élément d'une liste, il faut utiliser les
## doubles crochets [[ ]]. Les simples crochets [ ]
## fonctionnent aussi, mais retournent une sous-liste -- ce
## qui est rarement ce que l'on souhaite.
x[[1]] # premier élément de la liste...
mode(x[[1]]) # ... un vecteur
x[1] # aussi le premier élément...
mode(x[1]) # ... mais une sous-liste...
length(x[1]) # ... d'un seul élément
x[[2]][1] # 1er élément du 2e élément
x[[c(2, 1)]] # idem, par indiçage récursif
## Les éléments d'une liste étant généralement nommés (c'est
## une bonne habitude à prendre! ), il est souvent plus simple
## et sûr d'extraire les éléments d'une liste par leur
## étiquette.
x$joueur # équivalent à a[[1]]
x$score[1] # équivalent à a[[c(2, 1)]]
x[["expert"]] # aussi valide, mais peu usité
x$level <- 1 # aussi pour l'affectation
## Une liste peut contenir n'importe quoi...
x[[5]] <- matrix(1, 2, 2) # ... une matrice...
x[[6]] <- list(20:25, TRUE) # ... une autre liste...
x[[7]] <- seq # ... même le code d'une fonction!
x # eh ben!
x[[c(6, 1, 3)]] # de quel élément s'agit-il ?
## Pour supprimer un élément d'une liste, lui assigner la
## valeur 'NULL'.
x[[7]] <- NULL; length(x) # suppression du 7e élément
## Il est parfois utile de convertir une liste en un simple
## vecteur. Les éléments de la liste sont alors « déroulés », y
## compris la matrice en position 5 (qui n'est rien d'autre
## qu'un vecteur, on s'en souviendra).
unlist(x) # remarquer la conversion
unlist(x, recursive = FALSE) # ne pas appliquer aux sous-listes
unlist(x, use.names = FALSE) # éliminer les étiquettes
###
### DATA FRAMES
###
## Un data frame est une liste dont les éléments sont tous de
## même longueur. Il comporte un attribut 'dim', ce qui fait
## qu'il est représenté comme une matrice. Cependant, les
## colonnes peuvent être de modes différents.
(DF <- data.frame(Noms = c("Pierre", "Jean", "Jacques"),
Age = c(42, 34, 19),
Fumeur = c(TRUE, TRUE, FALSE)))
mode(DF) # un data frame est une liste...
class(DF) # ... de classe 'data.frame'
dim(DF) # dimensions implicites
names(DF) # titres des colonnes
row.names(DF) # titres des lignes (implicites)
DF[1, ] # première ligne
DF[, 1] # première colonne
DF$Noms # idem, mais plus simple
## Lorsque l'on doit travailler longtemps avec les différentes
## colonnes d'un data frame, il est pratique de pouvoir y
## accéder directement sans devoir toujours indicer. La
## fonction 'attach' permet de rendre les colonnes
## individuelles visibles dans l'espace de travail. Une fois
## le travail terminé, 'detach' masque les colonnes.
exists("Noms") # variable n'existe pas
attach(DF) # rendre les colonnes visibles
exists("Noms") # variable existe
Noms # colonne accessible
detach(DF) # masquer les colonnes
exists("Noms") # variable n'existe plus
###
### INDIÇAGE
###
## Les opérations suivantes illustrent les différentes
## techniques d'indiçage d'un vecteur pour l'extraction et
## l'affectation, c'est-à-dire que l'on utilise à la fois la
## fonction '[' et la fonction '[<-'. Les mêmes techniques
## existent aussi pour les matrices, tableaux et listes.
##
## On crée d'abord un vecteur quelconque formé de vingt
## nombres aléatoires entre 1 et 100 avec répétitions
## possibles.
(x <- sample(1:100, 20, replace = TRUE))
## On ajoute des étiquettes aux éléments du vecteur à partir
## de la variable interne 'letters'.
names(x) <- letters[1:20]
## On génère ensuite cinq nombres aléatoires entre 1 et 20
## (sans répétitions).
(y <- sample(1:20, 5))
## On remplace maintenant les éléments de 'x' correspondant
## aux positions dans le vecteur 'y' par des données
## manquantes.
x[y] <- NA
x
## Les cinq méthodes d'indiçage de base.
x[1:10] # avec des entiers positifs
"["(x, 1:10) # idem, avec la fonction '['
x[-(1:3)] # avec des entiers négatifs
x[x < 10] # avec un vecteur booléen
x[c("a", "k", "t")] # par étiquettes
x[] # aucun indice...
x[numeric(0)] # ... différent d'indice vide
## Il arrive souvent de vouloir indicer spécifiquement les
## données manquantes d'un vecteur (pour les éliminer ou les
## remplacer par une autre valeur, par exemple). Pour ce
## faire, on utilise la fonction 'is.na' et l'indiçage par un
## vecteur booléen. (Note : l'opérateur '! ' ci-dessous est la
## négation logique.)
is.na(x) # positions des données manquantes
x[!is.na(x)] # suppression des données manquantes
x[is.na(x)] <- 0; x # remplace les NA par des 0
"[<-"(x, is.na(x), 0) # idem, mais très peu usité
## On laisse tomber les étiquettes de l'objet.
names(x) <- NULL
## Quelques cas spéciaux d'indiçage.
length(x) # un rappel
x[1:25] # allonge le vecteur avec des NA
x[25] <- 10; x # remplit les trous avec des NA
x[0] # n'extrait rien
x[0] <- 1; x # n'affecte rien
x[c(0, 1, 2)] # le 0 est ignoré
x[c(1, NA, 5)] # indices NA retourne NA
x[2.6] # fractions tronquées vers 0
## On laisse tomber les 5 derniers éléments et on convertit le
## vecteur en une matrice 4 x 5.
x <- x[1:20] # ou x[-(21:25)]
dim(x) <- c(4, 5); x # ajouter un attribut 'dim'
## Dans l'indiçage des matrices et tableaux, l'indice de
## chaque dimension obéit aux mêmes règles que ci-dessus. On
## peut aussi indicer une matrice (ou un tableau) avec une
## matrice. Si les exemples ci-dessous ne permettent pas d'en
## comprendre le fonctionnement, consulter la rubrique d'aide
## de la fonction '[' (ou de 'Extract').
x[1, 2] # élément en position (1, 2)
x[1, -2] # 1re rangée sans 2e colonne
x[c(1, 3), ] # 1re et 3e rangées
x[-1, ] # supprimer 1re rangée
x[, -2] # supprimer 2e colonne
x[x[, 1] > 10, ] # lignes avec 1er élément > 10
x[rbind(c(1, 1), c(2, 2))] # éléments x[1, 1] et x[2, 2]
x[cbind(1:4, 1:4)] # éléments x[i, i] (diagonale)
diag(x) # idem et plus explicite
2-10. Exercices▲
-
Écrire une expression R pour créer la liste suivante :
Sélectionnez1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.>x[[1]][1]12345$data[,1][,2][,3][1,]135[2,]246[[3]]2.10. Exercices47[1]000$test[1]FALSEFALSEFALSEFALSE -
Trouver le mode et la longueur du quatrième élément de la liste.
-
Extraire les dimensions du second élément de la liste.
-
Extraire les deuxième et troisième éléments du second élément de la liste.
-
Remplacer le troisième élément de la liste par le vecteur
3:8.
2.2 (solution) Soit x un vecteur contenant les valeurs d'un échantillon :
2.
3.
> x
[1] 1 18 2 1 5 2 6 1 12 3 13 8 20 1 5 7
[17] 7 4 14 10
Écrire une expression R permettant d'extraire les éléments suivants :
-
le deuxième élément de l'échantillon ;
-
les cinq premiers éléments de l'échantillon ;
-
les éléments strictement supérieurs à 14 ;
-
tous les éléments sauf les éléments en positions 6, 10 et 12.
2.3 (solution) Soit x une matrice 10 × 7 obtenue aléatoirement avec
> x <- matrix(sample(1:100, 70), 7, 10)Écrire des expressions R permettant d'obtenir les éléments de la matrice demandés ci-dessous.
-
L'élément (4, 3).
-
Le contenu de la sixième ligne.
-
Les première et quatrième colonnes (simultanément).
-
Les lignes dont le premier élément est supérieur à 50.



