R et espace

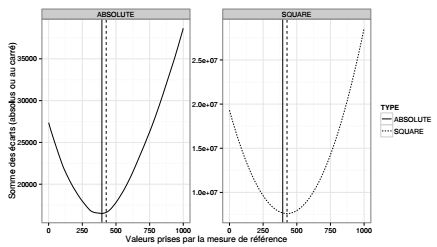
La moyenne, comme la médiane, est une mesure de centralité parce que la somme des écarts entre cette valeur et toutes les valeurs prises par la variable est minimale. Plus précisément, la moyenne est la valeur qui minimise la somme du carré des écarts (1), la médiane est la valeur qui minimise la somme de la valeur absolue des écarts (2).

Ces propriétés de la moyenne et de la médiane peuvent être testées sur une variable quantitative quelconque. Dans cet exemple, la variable utilisée est la capacité des hôpitaux (nombre de lits) de l'espace d'étude.

Dans un premier temps, cette variable est extraite de la table attributaire de l'objet spatial. La moyenne et la médiane de la variable sont calculées. La distribution est dissymétrique à gauche, la moyenne est supérieure à la médiane.

hospCapacity <- publicHosp$Capacite
meanCapacity <- mean(hospCapacity)
medCapacity <- median(hospCapacity)

Dans un deuxième temps, une séquence de valeurs est créée qui encadre les valeurs centrales, il s'agit d'une suite d'entiers entre 0 et 1000 avec un pas de 5. Ces 201 valeurs seront prises successivement comme valeur de référence : la somme des écarts entre chaque valeur de référence (kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp) et toutes les valeurs prises par la variable (kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp) sera calculée (écarts absolus et écarts au carré) avec une fonction de type apply() (cf. Section 3.4L'application de fonctions sur des ensembles). L'ensemble est enfin regroupé dans un tableau, c'est-à-dire les séquences de valeurs avec un pas de 5, les 201 sommes de la valeur absolue des écarts, les 201 sommes du carré des écarts et le type correspondant à ces calculs (absolute et square).

seqVec <- seq(0, 1000, 5)

absDif <- sapply(
    seqVec,
    function(x, xi = hospCapacity) sum(abs(xi - x))
)

squDif <- sapply(
    seqVec,
    function(x, xi = hospCapacity) sum((xi - x) ^ 2)
)

difCurves <- data.frame(
    SUMDIF = c(absDif, squDif),
    SEQVAL = c(seqVec, seqVec),
    TYPE = c(rep("ABSOLUTE", length(absDif)),
             rep("SQUARE", length(squDif)))
)

Enfin, la variable est représentée graphiquement avec le package ggplot2 (cf. Section 9.3Introduction à ggplot2) : la somme des écarts est représentée par une courbe, les valeurs de la moyenne et de la médiane sont représentées par des lignes verticales. On vérifie ici les propriétés de ces deux mesures de centralité qui correspondent au minimum de chacune des deux fonctions.

ggplot() +
  geom_path(data = difCurves,
            aes(x = SEQVAL, y = SUMDIF, linetype = TYPE)) +
  geom_vline(xintercept = medCapacity, linetype = 1) +
  geom_vline(xintercept = meanCapacity, linetype = 2) +
  facet_wrap(~ TYPE, scales = "free") +
  xlab("Valeurs prises par la mesure de référence") +
  ylab("Somme des écarts (absolus ou au carré)") +
  theme_bw()

medCapacity

## [1] 395.5

seqVec[ which.min(absDif)]

## [1] 395

Le raisonnement peut être appliqué d'un point de vue spatial dans un espace à une seule dimension. Le modèle de Hotelling en est un bon exemple : l'espace du modèle est une plage linéaire sans largeur où des vacanciers sont répartis de façon aléatoire(39). Sur cette plage, des vendeurs de glace cherchent à se rapprocher de leur clientèle potentielle. Le glacier qui veut maximiser ses opportunités de vente cherchera à se placer au point qui minimise la somme des distances à tous les vacanciers. Ce point est le point médian, il est facile à trouver dans un espace à une dimension, mais il est plus difficile à approcher dans un espace à deux dimensions.

Dans un espace à deux dimensions, la moyenne et la médiane restent des mesures de centralité très utilisées pour décrire un semis de points. Le point moyen, ou centre de gravité, ou barycentre, est le point qui minimise le carré des distances à tous les autres points. Le point médian, quant à lui, minimise la somme des distances à parcourir. Ce point est la solution de problèmes simples de localisation, il est connu sous le nom de « point de Weber », du nom de l'économiste Alfred Weber (frère de Max Weber) qui l'a défini dans un travail sur les localisations industrielles. D'autres points centraux peuvent être utilisés, en particulier le point minimax qui minimise la distance au point le plus éloigné.

Dans la suite de cette section, le point moyen et le point médian sont calculés sur les données de Paris et de la petite couronne : le point médian sur le semis des hôpitaux et le point moyen sur le semis des communes. Le premier calcul répond à la question d'un hypocondriaque extrémiste qui veut se situer au plus près de l'ensemble des hôpitaux. Le second calcul permettra de déterminer le centre géométrique de l'espace d'étude d'abord, son centre démographique ensuite, en prenant en compte la population des communes, enfin il permettra de voir le déplacement de ce centre au cours du temps.

Le point médian est d'abord approché par une méthode à la fois didactique et rudimentaire. Dans un premier temps les coordonnées des hôpitaux sont extraites de l'objet spatial grâce à la fonction coordinates(). Ensuite, l'étendue de l'espace d'étude (bounding box) est récupérée avec la fonction bbox(). Ces deux éléments serviront de base au calcul. La dernière ligne de code utilise la fonction fortify() pour extraire la géométrie du polygone (contour de l'espace d'étude) et pouvoir la représenter avec le package ggplot2 (cf. Section 9.3Introduction à ggplot2). Cette dernière étape n'est utile que pour la représentation cartographique, elle n'a pas de rôle à jouer dans le calcul du point médian.

coordHosp <- as.data.frame(coordinates(publicHosp))
colnames(coordHosp) <- c("COORDX", "COORDY")
bboxRegion <- bbox(regBoundary)
fortBoundary <- fortify(regBoundary)

Il s'agit ensuite de parcourir l'étendue de l'espace d'étude en s'arrêtant régulièrement pour prendre un point de référence et calculer la somme des distances entre ce point et l'ensemble des hôpitaux. Pour cela, une grille est créée, c'est-à-dire un semis de points régulier qui couvre l'étendue de l'espace d'étude. Pour créer cette grille, on parcourt l'étendue des x et l'étendue des y avec une séquence régulière (pas de 1000) avec le fonction seq(), puis ces deux séquences sont combinées avec la fonction expand.grid().

seqCoordX <- seq(floor(bboxRegion[ 1, 1]),
                 ceiling(bboxRegion[ 1, 2]),
                 by = 1000)

seqCoordY <- seq(floor(bboxRegion[ 2, 1]),
                 ceiling(bboxRegion[ 2, 2]),
                 by = 1000)

longGrid <- expand.grid(COORDX = seqCoordX,
                        COORDY = seqCoordY)

Finalement, une matrice de distances est calculée entre le semis de points des hôpitaux et le semis régulier (grille). C'est la fonction rdist() du package fields qui effectue ce travail. L'utilisateur pourrait envisager d'écrire lui-même une fonction qui calcule la matrice de distances, cependant une fonction de ce type est rapidement gourmande en calcul et il vaut mieux utiliser une fonction, telle que rdist(), qui est programmée en Fortran et qui sera bien plus rapide qu'une fonction programmée en R (cf. Section 3.3.1Premier aperçu sur les fonctions).

library(fields)
matDist <- rdist(coordHosp, longGrid)
sumDist <- apply(matDist, 2, sum)
longGrid$ABSDIST <- sumDist

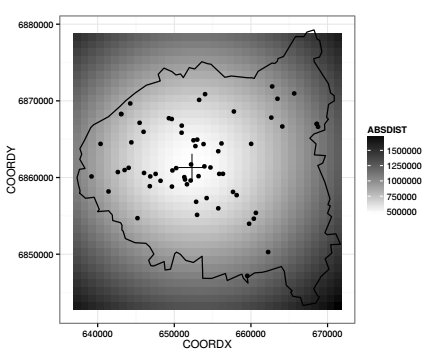
Le résultat est cartographié avec ggplot2. Quatre couches sont superposées : la première est une grille (raster) dont chaque pixel représente la somme des distances entre ce pixel et l'ensemble des points qui forment le semis des hôpitaux, la deuxième est une croix correspondant au point pour lequel cette somme est minimale (approximation du point médian), la troisième est le semis des hôpitaux, la quatrième est le contour de l'espace d'étude.

ggplot() +
  geom_raster(data = longGrid,
              aes(x = COORDX, y = COORDY, fill=ABSDIST)) +
  geom_point(data = longGrid[ which.min(longGrid$ABSDIST),],
             aes(x = COORDX, y = COORDY),
             colour = "black", shape = 3, size = 10) +
  geom_point(data = coordHosp,
             aes(x = COORDX, y = COORDY),
             colour = "black", size = 2) +
  geom_polygon(data = fortBoundary,
               aes(x = long, y = lat, group = group),
               fill = NA, colour = "black") +
  scale_fill_gradientn(colours = c("white", "black")) +
  coord_equal() +
  theme_bw()

Il serait possible avec l'algorithme développé ci-dessus de donner une approximation plus précise du point médian en fixant une résolution plus fine à la grille, mais les calculs deviendraient rapidement très lourds. Il existe bien sûr des méthodes bien plus élégantes et plus efficientes pour calculer le point médian, l'algorithme le plus classique étant implémenté dans plusieurs packages de R, par exemple dans le package ICSNP.

library(ICSNP)
spatial.median(coordHosp)

## COORDX COORDY
## 652242 6861734

L'une des caractéristiques de la moyenne vis-à-vis de la médiane est d'être plus sensible aux variations de valeur, que ce soit dans un espace à une ou à deux dimensions. Cette caractéristique peut s'avérer intéressante lorsqu'on cherche à mettre en évidence des évolutions temporelles et le point moyen est souvent utilisé de la sorte.

Il s'agit dans l'exemple suivant de calculer le point moyen sur le semis des communes, du centroïde des communes plus précisément, mais en tenant compte du poids de chaque commune en termes de population. Ce qui est calculé est donc un point moyen pondéré par la population, et ce point moyen sera calculé pour chacune de dates auxquelles on dispose d'une variable de population entre 1936 et 2008. Les coordonnées de ce point moyen ou centre de gravité (kitxmlcodeinlinelatexdvpx_gfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpy_gfinkitxmlcodeinlinelatexdvp) se calculent en faisant la moyenne pondérée (kitxmlcodeinlinelatexdvpw_ifinkitxmlcodeinlinelatexdvp) des coordonnées des points (kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpy_ifinkitxmlcodeinlinelatexdvp)

Les coordonnées des centroïdes des communes sont extraites de l'objet spatial avec la fonction coordinates() et le code des communes est récupéré dans la table attributaire de cet objet. Ensuite, une jointure est faite avec le tableau popCom3608 qui contient les variables de population à différentes dates.

coordMuni <- data.frame(X = coordinates(muniBound)[ , 1],
                        Y = coordinates(muniBound)[ , 2],
                        CODGEO = muniBound@data$INSEE_COM,
                        stringsAsFactors = FALSE)

coordPop <- merge(coordMuni, popCom3608,
                  by = "CODGEO",
                  sort = TRUE)

Pour calculer automatiquement les points moyens à chaque date, une boucle est mise en place. Les fonctions de type apply() sont souvent meilleures que les boucles pour appliquer une fonction successivement à un ensemble (cf. Section 3.4L'application de fonctions sur des ensembles). Elles sont meilleures à la fois en termes de vitesse d'exécution et en termes de lisibilité du code. Cependant, en termes de vitesse leur supériorité dépend en grande partie du nombre de cas auxquels la fonction est appliquée. Sur un très petit nombre comme ici (9 dates de recensement), ce différentiel de vitesse est nul. En outre, il semble plus facile dans ce cas d'écrire un code simple et lisible au travers d'une boucle.

Deux vecteurs vides sont créés pour stocker les valeurs successives des coordonnées x et y du centre de gravité. La boucle fera neuf itérations et i prendra successivement les valeurs entières comprises entre 5 et 13, ce qui correspond à l'index des colonnes contenant les populations à chaque date. À la fin de chaque itération, les valeurs des coordonnées seront ajoutées aux vecteurs de stockage.

xgEvol <- vector()
ygEvol <- vector()

for(i in 5: 13){
    xgTemp <- weighted.mean(coordPop$X, w = coordPop[ , i])
    ygTemp <- weighted.mean(coordPop$Y, w = coordPop[ , i])
    xgEvol <- append(xgEvol, xgTemp)
    ygEvol <- append(ygEvol, ygTemp)
}

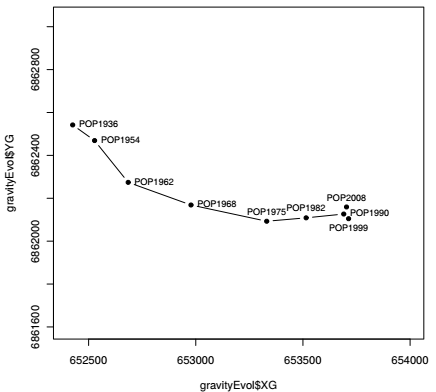
Les coordonnées du centre de gravité sont stockées dans un tableau qui peut maintenant être cartographié, avec la fonction générique plot() dans l'exemple ci-dessous. Les arguments utilisés ont déjà été vus dans les chapitres antérieurs : type pour le type du tracé (point, line, both), pch pour le type de point (point character) et asp pour le ratio d'échelle entre les axes x et y.

gravityEvol <- data.frame(YEAR = colnames(coordPop)[ 5: 13],
                          XG = xgEvol,
                          YG = ygEvol)

plot(gravityEvol$XG, gravityEvol$YG,
     type = "b",
     pch = 20,
     asp = 1,
     xlim = c(652400, 654000))

text(x = gravityEvol$XG,
     y = gravityEvol$YG,
     labels = gravityEvol$YEAR,
     cex = 0.8, pos = c(rep(4, 4), rep(3, 2), 4, 1, 3))

Ce graphique peut être brièvement commenté : durant la première moitié du XX^e siècle, l'Ouest de l'agglomération s'est peuplé plus rapidement que l'Est, tendance qui s'est inversée durant la seconde moitié du siècle. Le centre de gravité pondéré par la population s'est donc déplacé vers l'Est durant la période 1936-2008, résultat cohérent avec les analyses faites à la Section 6.1Analyse en composantes principales. Ni le contour de l'espace d'étude, ni les limites municipales n'ont été ajoutées à cette carte parce que l'étendue de ce déplacement reste limitée : entre 1936 et 2008, le centre de gravité traverse le 4^e arrondissement d'Est en Ouest.

Lorsque l'on dispose d'un semis de points, la description de la structure de répartition du semis se fonde sur des mesures de l'espacement entre les points, résumés à l'ensemble du semis. Dans ces approches, la distance joue un rôle fondamental. Il y a plusieurs façons de mesurer l'éloignement entre deux points, c'est ici la façon la plus simple qui est utilisée : la distance euclidienne à vol d'oiseau. Pour certaines questions, il peut être nécessaire d'utiliser une distance plus appropriée.

À la base de la description des espacements entre points du semis, il faut calculer une matrice de distance entre tous les points, comme cela a été fait dans la section précédente. Il est courant de travailler non sur l'ensemble de la matrice, mais sur la notion de distance au plus proche voisin. Cette distance peut aussi être généralisée à des ordres supérieurs par exemple la distance moyenne aux 3 ou aux 5 plus proches voisins.

La distance au plus proche voisin peut être utilisée dans un cadre descriptif pour décrire des contextes locaux. Elle peut aussi être utilisée dans une approche modélisatrice, par exemple comme variable explicative dans une régression multiple. Elle peut enfin être utilisée pour caractériser le semis de points en le comparant à une distance théorique obtenue par un processus ponctuel aléatoire, un processus de Poisson par exemple.

Le calcul de la distance moyenne au plus proche voisin peut être traité de deux façons :

• calculer une matrice de distance entre tous les points ou distancier (cf. Section 3.1.2Exemple 2 : double boucle for). Cette méthode a l'avantage de créer un objet complet à partir duquel un grand nombre d'indicateurs peuvent être calculés (distance au plus proche voisin, distance moyenne à tous les voisins). Elle a cependant l'inconvénient de créer un objet surdimensionné par rapport à l'utilisation que l'on peut en faire, objet qui peut être très lourd si le semis comporte un très grand nombre de points ;
• utiliser une suite de fonctions implémentées dans le package spdep spécialisé dans les statistiques spatiales. L'inconvénient de cette méthode est qu'il faut manipuler des types d'objets spécifiques avec des fonctions qui souvent ne servent qu'à passer d'un type d'objet à un autre.

Le distancier est calculé à partir des coordonnées contenues dans le tableau de données en utilisant la fonction dist(). Plusieurs distances sont proposées (distance de Manhattan, de Canberra, etc.), c'est ici la distance euclidienne qui est choisie. Utilisée comme suit, elle permet de construire le triangle inférieur hors diagonale d'une matrice de distance. Elle contient dans ce cas kitxmlcodeinlinelatexdvpn(n-1)/2finkitxmlcodeinlinelatexdvp éléments. Il faut ensuite transformer cet objet en un objet matrice kitxmlcodeinlinelatexdvpn\times nfinkitxmlcodeinlinelatexdvp en utilisant la fonction as.matrix().

distHosp <- dist(coordHosp, method = "euclidean")
matDistHosp <- as.matrix(distHosp)

On effectue ensuite le calcul de la distance au plus proche voisin pour chaque hôpital en ayant eu soin au préalable d'éliminer du calcul les éléments de la diagonale (en leur donnant la valeur NA), sans quoi chaque hôpital serait son plus proche voisin à une distance de 0.

matDistHosp[matDistHosp == 0] <- NA
minDist <- apply(matDistHosp, 1, min, na.rm = TRUE)
mean(minDist)

## [1] 1392

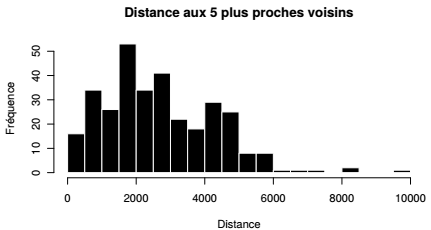
La valeur moyenne de la distance au plus proche voisin est donc de 1392 mètres. Indépendamment de la méthode des plus proches voisins, on peut s'intéresser à différentes statistiques des distances de chaque hôpital aux autres, en effectuant des statistiques univariées sur chacune des distributions. Les lignes qui suivent permettent de créer un tableau à n lignes et 7 colonnes pour les différents indicateurs créés par la fonction summary(). Ce tableau peut être transposé et trié pour en faciliter la lecture.

summaryDist <- apply(matDistHosp, 1, summary, na.rm = TRUE)
head(t(summaryDist))

##   Min. 1st Qu. Median  Mean 3rd Qu.  Max. NA's
## 1 1180    4190   8060  8000   11300 16900   1
## 2  922    6020   8040  9130   11800 21400   1
## 3  324    4560   7510  8090   11200 18700   1
## 4 4130   13900  17500 16900   21300 26400   1
## 5 1450    5120   8110  9350   12700 19100   1
## 6 2020    5890   9440 10300   14100 18000   1

Le package spdep contient un ensemble de fonctions dédiées aux statistiques spatiales. Ces fonctions créent des objets spécifiques, par exemple des listes de voisins, qui doivent souvent être transformées pour alimenter d'autres fonctions du package, par exemple pour représenter graphiquement les points et leurs voisins.

Dans un premier temps, la fonction knearneigh() permet de calculer de manière générique la liste des k plus proches (near) voisins (neighbours) d'un ensemble. Lorsque cette fonction est appliquée à un objet spatial, la fonction récupère directement l'ensemble des informations nécessaires aux calculs et travaille sur le vecteur $coords. La proximité est ici entendue au sens de la distance euclidienne. Si on spécifie l'argument longlat, la fonction peut aussi faire le calcul sur des coordonnées géographiques (longitudes-latitudes) en degrés décimaux. Dans cet exemple, on commence par créer une liste de plus proches voisins d'ordre 5 (argument k).

library(spdep)
listNearNei <- knearneigh(publicHosp@coords, k = 5)
class(listNearNei)

L'objet qui vient d'être créé est une liste de type knn dont le premier élément est le vecteur des plus proches voisins. Ce schéma résume les types d'objets manipulés avec spdep et les fonctions qui assurent leur transformation.

Le premier élément de cet objet knn est, pour chaque hôpital, la liste des cinq hôpitaux les plus proches. À partir de cet objet, la distance est calculée entre chaque hôpital et ses cinq plus proches voisins grâce à la fonction nbdists(). Ce calcul ne peut être fait directement sur l'objet knn et il faut le transformer en objet de type nb. La fonction nbdists() demande également de préciser les coordonnées des hôpitaux contenues dans l'objet spatial (@coords).

nearNei <- knn2nb(listNearNei,
                  row.names = publicHosp$CodHop)

distNei <- nbdists(nearNei, publicHosp@coords)
class(distNei)

La structure de liste renvoyée par la fonction nbdists() est simplifiée avec la fonction unlist() qui crée un vecteur numérique regroupant toutes les distances. Ce vecteur donne la distance entre tous les couples d'hôpitaux voisins à un ordre 5. Cette variable peut être explorée avec les méthodes présentées dans le Chapitre 4CHAPITRE 4 Analyse univariée.

distNei <- unlist(distNei)
summary(distNei)

## Min. 1st Qu. Median Mean 3rd Qu. Max.
##    0    1550   2450 2700    3890 9580

hist(distNei, breaks = 20,
     main = "Distance aux 5 plus proches voisins",
     col = "black",
     border = "white",
     xlab = "Distance",
     ylab = "Fréquence")

Il est parfois intéressant de fixer une distance seuil et non un nombre fixe de voisins. Par exemple, en définissant un seuil de 2 km, il est possible de créer, pour chacun des points, une liste de voisins situés à une distance inférieure à deux kilomètres. La fonction dnearneigh() crée cette liste, à partir des coordonnées des points et des seuils de distance (arguments d1 et d2), ici de 0 à 2000 mètres.

neiTwoKm <- dnearneigh(publicHosp@coords,
                       d1 = 0,
                       d2 = 2000,
                       row.names=publicHosp$CodHop)

Cette fonction renvoie directement un objet de type nb.

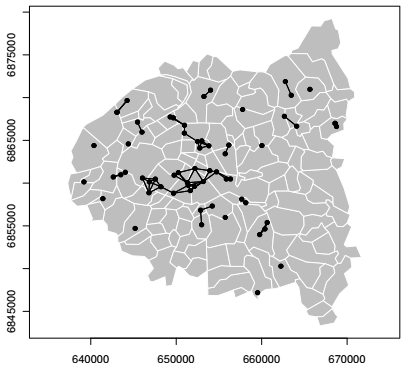
Il est utile de compléter les mesures qui viennent d'être calculées avec des représentations cartographiques. Les objets de types nb, qui sont des listes de voisins, peuvent être représentés sous la forme de graphes et ajoutés à la cartographie du semis de points. L'exemple ci-dessous montre les réseaux de voisins à une distance inférieure à deux kilomètres.

plot(muniBound, axes = TRUE,
     col = "grey", border = "white")
plot(publicHosp, col = "black", pch = 20, add = TRUE)
plot(neiTwoKm, publicHosp@coords,
     pch = 20, col = "black", add = TRUE)

Les méthodes de statistique spatiale qui viennent d'être introduites s'appliquent à des semis de points. Il existe également toute une gamme de méthodes qui s'appliquent à des phénomènes observés dans des zones, par exemple dans des maillages territoriaux. L'autocorrélation spatiale en fait partie, elle sera travaillée ici sur le maillage communal.

L'autocorrélation spatiale consiste, pour un phénomène donné, à mesurer l'intensité de la relation entre la proximité des lieux et leur degré de ressemblance au regard de ce phénomène. Le fondement de ces mesures est la mise en rapport d'une variabilité locale avec la variabilité globale.

Les premiers développements de ces mesures concernaient des voisinages définis par la contiguïté sur un maillage. La variance locale peut alors s'écrire comme une variance globale pondérée par un poids wij affecté à chacun des couples kitxmlcodeinlinelatexdvp(i, j) : w_{ij} = 1finkitxmlcodeinlinelatexdvp si kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp sont des zones contiguës, kitxmlcodeinlinelatexdvpw_{ij} = 0finkitxmlcodeinlinelatexdvp sinon. Dans ce cas kitxmlcodeinlinelatexdvpwfinkitxmlcodeinlinelatexdvp est une matrice de contiguïté.

Ce principe peut être étendu à la notion de voisinage au sens large, en considérant comme voisines des unités spatiales distantes de moins de 5 km, de moins d'une heure ou appartenant à la même région administrative. Dans ce cas, kitxmlcodeinlinelatexdvpw_{ij}finkitxmlcodeinlinelatexdvp sera aussi une variable binaire et kitxmlcodeinlinelatexdvpwfinkitxmlcodeinlinelatexdvp une matrice de contiguïté. Il est enfin possible de pondérer les couples par l'inverse de la distance (ou du temps), auquel cas kitxmlcodeinlinelatexdvpw_{ij}finkitxmlcodeinlinelatexdvp sera une variable continue et w une matrice de poids.

Les deux indices d'autocorrélation les plus anciens et les plus utilisés sont l'indice I de Moran (1950) et l'indice C de Geary (1954).

Où kitxmlcodeinlinelatexdvpNfinkitxmlcodeinlinelatexdvp est le nombre d'individus, kitxmlcodeinlinelatexdvpX_ifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpX_jfinkitxmlcodeinlinelatexdvp sont les valeurs de la variable

kitxmlcodeinlinelatexdvpXfinkitxmlcodeinlinelatexdvp en kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp, kitxmlcodeinlinelatexdvp\bar{X}finkitxmlcodeinlinelatexdvp est la moyenne de la variable kitxmlcodeinlinelatexdvpXfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpw_{ij}finkitxmlcodeinlinelatexdvp est une pondération correspondant à la définition du voisinage.

Des développements ont ensuite été proposés pour travailler sur les contributions locales des zones à cette mesure de l'autocorrélation spatiale. Il s'agit des indicateurs locaux d'association spatiale (LISA - local indicators of spatial autocorrelation). L'indice local de Moran correspond ainsi à la contribution de chaque unité à l'autocorrélation globale.

Il s'agit, pour une unité spatiale kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, du produit entre l'écart à la moyenne de cette unité spatiale (kitxmlcodeinlinelatexdvpz_ifinkitxmlcodeinlinelatexdvp) et la somme des écarts des unités voisines (kitxmlcodeinlinelatexdvpz_jfinkitxmlcodeinlinelatexdvp) pondérés par la matrice de contiguïté ou de poids (kitxmlcodeinlinelatexdvpw_{ij}finkitxmlcodeinlinelatexdvp).

Cet indicateur permet d'identifier les situations localement homogènes (kitxmlcodeinlinelatexdvpI_ifinkitxmlcodeinlinelatexdvp faible), et les situations localement hétérogènes (kitxmlcodeinlinelatexdvpI_ifinkitxmlcodeinlinelatexdvp élevé). Selon le phénomène étudié, on cherchera à isoler l'une et/ou l'autre de ces situations.

L'exemple suivant cherche à caractériser la répartition spatiale des cadres et des ouvriers dans l'espace d'étude.

La fonction moran.test() du package spdep travaille directement sur les objets de type nb qui donnent la liste des unités voisines. Pour travailler sur un objet de ce type, il faut au préalable transformer l'objet spatial contenant le découpage communal (SpatialPolygonsDataFrame) en objet de type nb.

C'est la fonction poly2nb() qui effectue ce travail. Plusieurs arguments doivent être précisés : l'argument queen (déplacement de la reine au jeu d'échecs) indique qu'un seul sommet commun entre deux polygones est suffisant pour les considérer comme voisins ou qu'il faut un segment commun. L'argument snap permet de fixer la distance en dessous de laquelle deux points d'un polygone sont considérés comme étant superposés. En effet, il arrive souvent de travailler avec des géométries de mauvaise qualité (erreurs de topologie), où les sommets formant des segments ne coïncident pas exactement.

Dans un premier temps, les variables du tableau externe socEco9907 sont jointes aux données attributaires de l'objet spatial. Cette manipulation est faite avec la fonction AttribJoin() créée dans le chapitre précédent (cf. Section 10.4.1Cartographie avec la fonction plot()). Ensuite, l'objet nb est créé. Enfin l'indice de Moran est calculé sur les deux variables mentionnées : la proportion de cadres et la proportion d'ouvriers dans les communes. La fonction moran.test() prend comme argument la variable à l'étude et la matrice de contiguïté ou de poids. Celle-ci est créée directement avec la fonction nb2listw().

muniBound <- AttribJoin(df = socEco9907,
                        spdf = muniBound,
                        df.field = "CODGEO",
                        spdf.field = "INSEE_COM")

nbCom <- poly2nb(pl = muniBound,
                 row.names = muniBound$INSEE_COM,
                 snap = 50,
                 queen = TRUE)

moran.test(x=muniBound$PCAD07,
           listw = nb2listw(nbCom))

moran.test(x=muniBound$POUV07,
           listw = nb2listw(nbCom))

La fonction renvoie la valeur de l'autocorrélation spatiale (0,75 pour les cadres et 0,69 pour les ouvriers), la valeur de l'écart standardisé (14,59 et 13,43) ainsi que la p-value. La proportion de cadres et la proportion d'ouvriers présentent une autocorrélation positive, synonyme dans ce cas de ségrégation spatiale.

Les valeurs de l'indice de Moran peuvent être représentées graphiquement et cartographiquement. Ici la relation est représentée par un nuage de points (Moran scatterplot) croisant les valeurs en i avec la moyenne des valeurs du voisinage de i.

La fonction moran.plot() demande, comme la fonction moran.test(), une matrice de poids. Celle-ci est produite, comme précédemment, par la fonction nb2listw(). L'argument style est précisé même s'il s'agit de sa valeur par défaut : il indique que les poids doivent être standardisés par lignes. C'est cet argument qui permet de lire les valeurs sur l'axe y du graphique comme une moyenne pondérée par la distance de la variable à l'étude.

moran.plot(x = muniBound$PCAD07,
           listw = nb2listw(nbCom, style = "W"),
           xlab = "% de cadres en 2007",
           ylab = "% de cadres dans le voisinage")

moran.plot(x = muniBound$POUV07,
           listw = nb2listw(nbCom, style = "W"),
           xlab = "% d'ouvriers en 2007",
           ylab = "% d'ouvriers dans le voisinage")

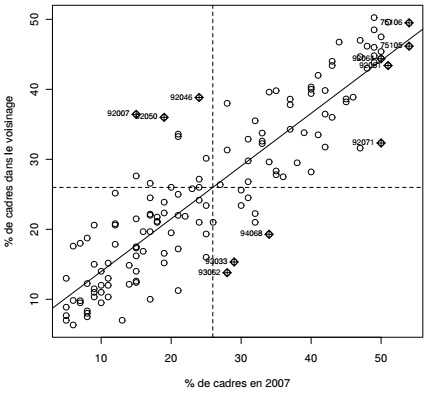
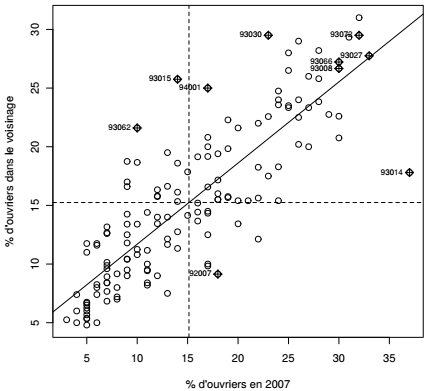
Ce type de graphique est très riche, il permet de visualiser l'autocorrélation, de classer les unités spatiales en termes de profils et de détecter les cas exceptionnels. Les droites horizontale et verticale sont centrées sur les moyennes de chacune des deux variables : ces droites dessinent des quadrants. Là encore, il sera intéressant de cartographier ces profils(40).

Pour la proportion de cadres par exemple, ces quadrants guideront la lecture en distinguant les communes comportant peu de cadres et peu de cadres dans le voisinage, les communes comportant beaucoup de cadres et beaucoup de cadres dans le voisinage. Les quadrants opposés sont particulièrement intéressants puisqu'ils montrent les discontinuités : les communes comportant beaucoup de cadres situées dans un voisinage qui en comportent peu (Saint-Maur-des-Fossés par exemple, code 94068) et celles qui comportent très peu de cadres dans un voisinage qui en comporte beaucoup (Bagneux par exemple, code 92007).

Ce chapitre a présenté des techniques simples d'analyse spatiale, techniques permettant de caractériser la répartition spatiale d'objets et de phénomènes. Les mesures de centralité, point moyen et point médian, peuvent servir à résumer la distribution d'un semis de points dans une approche descriptive, elles peuvent être utilisées pour saisir des évolutions du semis de point, elles peuvent enfin être utilisées dans un cadre opérationnel (localisation optimale pour un hôpital). Les fonctions du package spdep sont très intéressantes pour analyser plus finement les phénomènes spatiaux, par exemple la répartition des semis de points ou l'homogénéité d'un phénomène observé dans des unités spatiales.