III. CHAPITRE 3 Introduction à la programmation▲
Objectifs
Ce chapitre explique les principales procédures de programmation avec R : les structures itératives, les structures conditionnelles et les fonctions. Cette introduction à la programmation procure une grande souplesse dans la manipulation des données et permet d'automatiser de nombreuses procédures.
Prérequis
Notions de base du fonctionnement de R et de l'interface RStudio, telles que présentées dans les Chapitres 1CHAPITRE 1 Prise de contact et 2CHAPITRE 2 Prise en main et manipulation des données.
Description des pakages utilisés
Les manipulations effectuées dans ce chapitre ne nécessitent pas l'utilisation de packages particuliers.
III-A. Structures itératives▲
Les structures itératives et les structures conditionnelles sont les briques élémentaires les plus simples des algorithmes. Les boucles while et for permettent de répéter des instructions, le test conditionnel if...else permet d'effectuer des instructions en fonction de l'état des variables à un moment donné.
La boucle for, « pour chacun de », permet de répéter une instruction sur un nombre d'itérations déterminé à l'avance. La boucle while, « tant que », permet de répéter une instruction tant qu'une certaine condition est vérifiée. Ainsi, la boucle for est un cas particulier d'une boucle while : elle est plus simple à utiliser et peut être préférée dans la plupart des cas. Voici la pseudosyntaxe correspondant à ces deux structures itératives :
2.
3.
4.
5.
6.
7.
8.
9.
for (i in 1:n)
{
instruction répétée n fois
i prendra successivement toutes les valeurs entières
comprises entre 1 et n
}
while (condition d'arrêt) {
instruction
}
Les exemples d'application qui suivent présentent l'utilisation de ces structures itératives par ordre de difficulté croissant. Certains utilisent les données déjà manipulées dans les chapitres précédents sur les communes de Paris et petite couronne.
2.
3.
4.
5.
6.
7.
popCom3608 <- read.csv("data/PopCom3608.csv",
sep = ";",
stringsAsFactors = FALSE)
socEco9907 <- read.csv("data/SocEco9907.csv",
sep = ";",
stringsAsFactors = FALSE)
III-A-1. Exemple 1 : simple boucle for▲
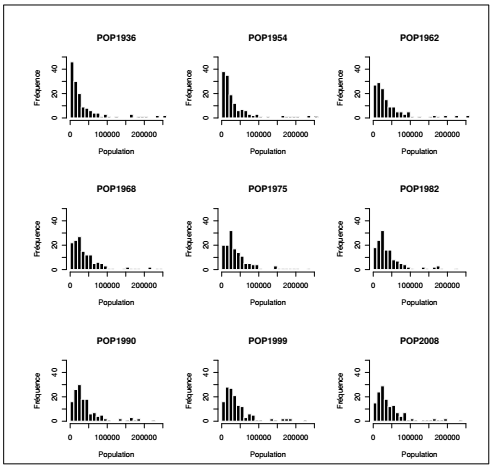
À partir des données de population des recensements de 1936 à 2008, on souhaite explorer par des graphiques, chacune des années du recensement sans avoir à réécrire la ligne de code pour chaque année. L'instruction doit être comprise de la façon suivante : pour chacune des colonnes du tableau entre 3 et 11 (toutes les variables de population), afficher l'histogramme correspondant. L'instruction suivante contient l'essentiel :
2.
3.
for(i in 3: 11){
hist(popCom3608[ , i])
}
Les arguments supplémentaires utilisés ici servent à personnaliser l'apparence des graphiques (cf. Chapitre 9CHAPITRE 9 Focus sur la visualisation graphique). La fonction par() fixe les paramètres d'affichage graphique, dans le cas suivant les neuf graphiques seront affichés en ligne sur une grille de 3 lignes par 3 colonnes. Les arguments de la fonction hist() servent à afficher le nombre de barres (breaks), le titre (main), la couleur de remplissage (col) et de bordure (border), les limites pour les axes (xlim et ylim) ainsi que les titres des axes (xlab et ylab).
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. |
Cette série de graphiques montre le peuplement progressif de la proche banlieue parisienne. Sur les 143 communes que compte l'espace d'étude, en 1936 presque la moitié étaient peuplées de moins de 10 000 habitants. Au cours du XXe siècle la distribution de la population est modifiée et ce sont les communes moyennes, de 20 000 à 40 000 habitants, qui deviennent majoritaires.
III-A-2. Exemple 2 : double boucle for▲
Cet exemple consiste à calculer un distancier entre communes à partir des coordonnées stockées dans le tableau socEco9907. Pour cela, on parcourt deux fois la table dans deux boucles imbriquées, afin de traiter tous les couples possibles de communes. L'indexation des lignes et des colonnes du tableau est utilisée pour parcourir le tableau en utilisant la syntaxe présentée dans la Section 2.1Description et manipulation des objets, le terme monTableau[i, j] désignant la ie ligne et la je colonne. Dans cet algorithme, on utilise les colonnes suivantes :
- la colonne 1 contient la liste des identifiants des communes ;
- la colonne 3 contient les coordonnées X des communes ;
- la colonne 4 contient les coordonnées Y des communes.
Les deux méthodes suivantes génèrent un distancier dans deux formats différents. Le premier exemple crée un format long qui prend la forme d'un tableau à trois colonnes (Comi - Comj - Distij). Le second exemple crée un format large qui prend la forme d'une matrice carrée dont les 143 lignes sont les communes d'origine, les 143 colonnes sont les communes de destination et les valeurs sont les distances pour chaque couple de commune. Le passage d'un format à l'autre ne pose aucun problème grâce aux fonctions présentées dans la Section 2.4.3Transposition variables-observations.
Pour construire un tableau en format long, on créé d'abord trois vecteurs vides : deux pour stocker les identifiants des communes et un pour stocker la distance entre chaque couple de communes.
2.
3.
commA <- vector()
commB <- vector()
distAB <- vector()
Puis, on remplit ces vecteurs progressivement à l'aide d'une double boucle for qui calcule, à chaque itération, la distance euclidienne entre un couple de communes(9). L'approche retenue ici consiste à utiliser un compteur numérique, k, qui est mis à jour à chaque passage dans la boucle la plus petite.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
k <- 1
n <- nrow(socEco9907)
for(i in 1: (n-1)) {
for(j in (i+1) : n) {
commA[k] <- socEco9907[i, 1]
commB[k] <- socEco9907[j, 1]
distAB[k] <- sqrt((socEco9907[i, 3] - socEco9907[j, 3]) ^2 +
(socEco9907[i, 4] - socEco9907[j, 4]) ^2)
k <- k + 1
}
}
Une fois remplis ces trois vecteurs, ils sont réunis dans un même tableau qui contiendra 3 colonnes et 10 153 lignes correspondant aux couples uniques de communes et excluant la distance d'une commune à elle-même (diagonale de la matrice dans l'exemple 2).
2.
3.
4.
5.
6.
7.
distCom <- data.frame(COMA = commA,
COMB = commB,
DISTANCE = distAB)
dim(distCom)
## [1] 10153 3
On crée dans ce second exemple une matrice origine-destination complète qui prendra la forme d'une matrice carrée et symétrique de 143 lignes et 143 colonnes. Cette approche consiste à créer une matrice vide, puis à la remplir par une double boucle.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
n <- nrow(socEco9907)
matDist <- matrix(0, nrow = n, ncol= n,
byrow=FALSE,
dimnames = list(socEco9907$CODGEO,
socEco9907$CODGEO))
for(i in 1: (n-1)) {
for(j in (i+1) : n) {
temp <- sqrt((socEco9907[i, 3] - socEco9907[j, 3]) ^2 +
(socEco9907[i, 4] - socEco9907[j, 4]) ^2)
matDist[i,j] <- temp
matDist[j,i] <- temp
}
}
dim(matDist)
## [1] 143 143
La construction d'un distancier par une double boucle est intéressante ici dans un cadre pédagogique, mais il s'agit d'une très mauvaise solution en termes de vitesse de calcul. C'est un cas typique dans lequel l'utilisation d'une fonction écrite dans un langage compilé sera bien meilleure (cf. Section 3.3.1Premier aperçu sur les fonctions), par exemple la fonction dist() ou la fonction rdist() du package fields.
III-B. La structure conditionnelle if…else▲
La fonction ifelse() présentée dans la Section 2.3Recoder et trier sert à assigner une valeur à une variable en fonction d'un test conditionnel et peut être appliquée sur un tableau directement. Il ne faut pas la confondre avec la structure conditionnelle if...else qui sert à exécuter des instructions en fonction du résultat du test. Cette structure peut tester une seule condition ou bien un enchaînement de conditions.
Cas 1 (un test conditionnel)
2.
3.
4.
5.
if (test) {
instructions si VRAI
} else {
instructions si FAUX
}
Cas 2 (deux tests conditionnels)
2.
3.
4.
5.
6.
7.
if (test1) {
instructions si VRAI test1
} else if (test2) {
instructions si VRAI test2
} else {
instructions si FAUX test1 et test2
}
La structure if...else est le plus souvent utilisée dans une boucle ou dans une fonction. C'est l'exemple présenté dans la section suivante.
III-C. Les fonctions▲
Il y plusieurs raisons qui peuvent motiver la conception de fonctions propres à l'utilisateur, voici les principales : si ce dernier doit répéter plusieurs fois la même procédure et ne souhaite pas réécrire à chaque fois le code correspondant, s'il veut rendre la procédure plus générique et pas seulement appliquée à des données particulières, si la procédure qu'il a mise au point est suffisamment générique et utile et qu'il souhaite la mettre à disposition d'autres utilisateurs. Les fonctions sont des « boîtes » auxquelles on donne des valeurs d'entrée (arguments de la fonction) et desquelles on retire des valeurs de sortie (résultats de la fonction). Avec R, il n'y a pas de contraintes fortes sur les types d'objets qui peuvent être en argument ou en sortie d'une fonction.
III-C-1. Premier aperçu sur les fonctions▲
2.
3.
4.
MaFonction <- function(arguments) {
traitements
return(sorties)
}
Voici la syntaxe générale pour écrire une fonction. Exécuter ce bloc de code, « sourcer la fonction », crée un objet nommé MySum dans l'environnement de travail. Cet objet peut être utilisé comme n'importe quelle fonction prédéfinie dans R, en fournissant les arguments demandés (ici a et b) on peut afficher ou récupérer une sortie (ici la somme de a et b) :
2.
3.
4.
5.
6.
7.
8.
MySum <- function(a, b) {
sumAB <- a + b
return(sumAB)
}
MySum(2, 3)
## [1] 5
L'un des intérêts du logiciel libre (ouvert) vis-à-vis des logiciels propriétaires (fermés) est l'accès au code. Dans la pratique scientifique, l'utilisateur peut examiner précisément ce que fait un algorithme et s'il fait effectivement ce qu'il annonce. Pour voir le code d'une fonction R, il suffit d'exécuter la fonction sans les parenthèses ni les arguments.
matrix
plotLe code de la fonction matrix() permet de présenter l'intégration de plusieurs langages de programmation. Parmi les fonctions implémentées dans les packages disponibles sur le CRAN, certaines sont écrites entièrement avec R alors que d'autres font appel à du programme écrit dans des langages compilés qui produisent des exécutables très rapides, en particulier Fortran, C et C++. L'appel à ce type d'exécutables se fait avec différentes fonctions, en particulier .Internal(), .Primitive(), .Call() ou encore .Fortran().
Le code de la fonction plot() permet de présenter la notion de fonction générique. De nombreuses fonctions implémentées dans R ont un comportement différent selon le type d'objet auquel elles s'appliquent .Par exemple, la fonction plot() produit un nuage de points lorsqu'elle s'applique à un couple de vecteurs numériques, elle produit des graphiques d'aide à l'interprétation si l'argument est un objet de type lm (linear model, cf. Section 5.2.3Régression linéaire simple). Il en est de même de la fonction abline(), summary() et bien d'autres. La fonction applique des « méthodes » différentes selon le type d'objet donné en entrée. La fonction methods() renvoie la liste des différentes méthodes correspondant à une fonction :
methods(plot)L'utilisateur qui veut entrer dans le détail de la programmation objet avec R trouvera de nombreuses ressources en anglais. En français, elles sont plus rares, on citera en particulier les manuels en ligne de Christophe Genolini(10).
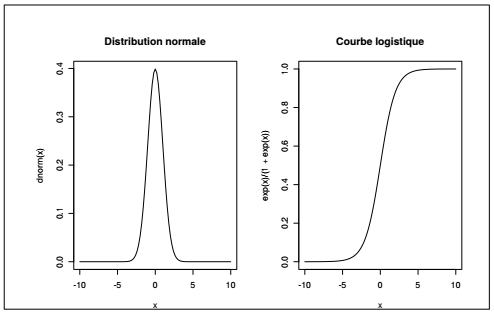
Les fonctions possèdent parfois des fonctionnalités de représentation graphique. La fonction curve() prend ainsi en argument une fonction et des bornes et affiche le graphique correspondant. À titre d'exemple, on peut représenter la densité de probabilité de la loi normale. Il est aussi possible de représenter graphiquement des fonctions définies directement en argument de la fonction curve(), x étant par défaut l'argument de la fonction mathématique qu'on souhaite représenter.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. |
|
|
Il est par ailleurs possible de dériver une fonction analytiquement dans R (et également de faire du calcul formel, c'est-à-dire de la manipulation analytique d'objets mathématiques) : par exemple, la dérivée de x → axb est x → abxb−1 ce que retrouve bien R. La possibilité de dériver des fonctions est rendue possible par la fonction D().
2.
3.
D(expression(a * x^b), "x")
## a * (x^(b - 1) * b)
Il est maintenant temps de créer des fonctions propres. Trois applications sont présentées dans les sections qui suivent : une fonction qui discrétise automatiquement une variable continue, une fonction qui calcule l'équilibre de Wardrop et une fonction qui calcule les vols de Syracuse.
III-C-2. Discrétisation automatique▲
La discrétisation de variables continues est une opération fréquente dans l'analyse de données géographiques. Elle est particulièrement utilisée pour la cartographie (cf. Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie). La méthode de discrétisation utilisée dépend de la distribution de la variable. Si cette distribution est normale, on discrétise souvent autour de la moyenne et de l'écart-type. En revanche si la distribution n'est pas normale, en particulier si elle est unimodale et très dissymétrique, on discrétise souvent en quantiles.
La fonction définie ci-dessous discrétise une variable continue en fonction d'un test de normalité : discrétisation autour de la moyenne si la distribution est normale, discrétisation en quartiles sinon.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
DiscretiMatic <- function (vec) {
normTest <- shapiro.test(vec)
if(normTest$p.value > 0.1) {
print("Discrétisation autour de la moyenne")
valBreaks <- c(min(vec),
mean(vec) - sd(vec),
mean(vec),
mean(vec) + sd(vec),
max(vec))
varDiscret <- cut(vec,
breaks = valBreaks,
include.lowest = TRUE,
right = FALSE)
} else {
print("Discrétisation en quartiles")
valBreaks <- quantile(vec,
probs = c(0, 0.25, 0.5, 0.75, 1))
varDiscret <- cut(vec,
breaks = valBreaks,
include.lowest = TRUE,
right = FALSE)
}
return(varDiscret)
}
popCom3608$POPDISCR36 <- DiscretiMatic(popCom3608$POP1936)
## [1] "Discrétisation en quartiles"
La fonction prend donc un vecteur numérique en entrée (argument) et renvoie un facteur en sortie. Elle produit au passage un message indiquant quelle méthode de discrétisation a été appliquée. Les fonctions peuvent être utilisées de toutes les façons possibles : une fonction peut exécuter des opérations et ne rien renvoyer en sortie, elle peut renvoyer des objets ou des listes d'objets en sortie, elle peut afficher des graphiques et des messages…
III-C-3. Calcul de l'équilibre de Wardrop▲
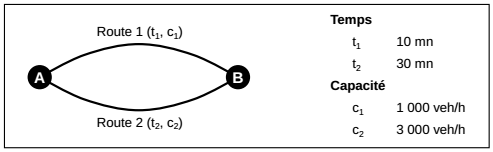
Deux routes permettent de se rendre du point A au point B. On cherche à savoir combien de personnes vont prendre chacune des deux routes sachant qu'elles ont des caractéristiques différentes en termes de temps de trajet (mesuré en minutes) et de capacité (mesuré en nombre maximum de véhicules par heure). La route 1 est plus courte, mais il ne s'agit que d'une route de faible capacité. La route 2 est une route de capacité plus importante, mais le temps de trajet est plus long que sur la route 1 (cf. Figure 3.1).
Si l'ensemble des 4000 véhicules cherche à prendre la route 1, celle-ci sera saturée et la vitesse plus faible. Si tout le monde prend la route 2, c'est une mauvaise stratégie puisqu'il existe une route inoccupée et plus rapide. Cet exercice consiste à trouver les flux optimaux sur chacune des deux routes, c'est-à-dire la répartition qui permet de minimiser le temps de transport total sur les deux routes.
On estime empiriquement que le temps de trajet dépend principalement de deux facteurs : le temps à vide, et la capacité de la route. Les flux sur les routes 1 et 2 sont respectivement notés q1 et q2, sachant que q1 + q2 égale le total de 4000 véhicules. Les temps de trajet varient en fonction de la congestion. Cette variation est documentée empiriquement depuis les années 1930 et formalisée par les équations suivantes (les équations et la valeur des paramètres sont des classiques du Bureau of Public Roads américain) :
kitxmlcodelatexdvpt1 = 10 * \left ( 1 + 0.15 * \left ( \frac{q1}{1000} \right )^4\right )finkitxmlcodelatexdvp kitxmlcodelatexdvpt2 = 30 * \left ( 1 + 0.15 * \left ( \frac{q2}{3000} \right )^4\right )finkitxmlcodelatexdvpEn application de la théorie économique dite de l'équilibre de Wardrop, dans la configuration qui minimise le temps de trajet des individus t1 = t2. Il faut donc trouver les valeurs de q1 et q2 qui assurent cette égalité. Autrement dit, on cherche x, nombre de voitures prenant la route 1, qui soit tel que :
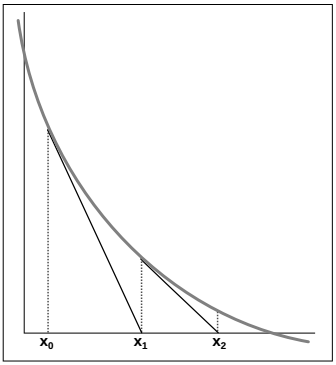
kitxmlcodelatexdvp10 * \left ( 1 + 0.15 * \left ( \frac{x}{1000} \right )^4\right ) - 30 * \left ( 1 + 0.15 * \left ( \frac{4000-x}{3000} \right )^4\right ) = 0finkitxmlcodelatexdvpIl s'agit de trouver kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp tel que kitxmlcodeinlinelatexdvpf(x) = 0finkitxmlcodeinlinelatexdvp pour une certaine fonction f. On décide d'une première estimation x 0 et on chercher ensuite successivement des estimations plus précises d'un x tel que kitxmlcodeinlinelatexdvpf(x) = 0finkitxmlcodeinlinelatexdvp par application de la méthode de Newton (cf. Figure 3.2). Si kitxmlcodeinlinelatexdvpx_0finkitxmlcodeinlinelatexdvp est la première estimation du nombre de voitures sur la route 1, et sous des conditions mathématiques qu'on espère ici vérifiées, kitxmlcodeinlinelatexdvpx_1 = x_0 - \frac{f'(x_0)}{f(x_0)}finkitxmlcodeinlinelatexdvp est une meilleure estimation encore du flux (kitxmlcodeinlinelatexdvpf'finkitxmlcodeinlinelatexdvp étant la dérivée de la fonction kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp). Et ainsi de suite : cette suite de valeurs converge vers la bonne solution. Il convient alors de définir la fonction kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp, sa dérivée, ainsi que la fonction de récurrence : kitxmlcodeinlinelatexdvpx_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}finkitxmlcodeinlinelatexdvp.
Dans l'exemple présenté ici cette convergence numérique est effective, mais il ne s'agit pas de démontrer que cette méthode marche dans tous les cas. Par ailleurs, dès lors qu'on cherche à affecter un trafic sur un réseau plus complexe, cette méthode ne peut s'appliquer et il faut avoir recours à des algorithmes spécifiques.
Dans un premier temps, les valeurs des constantes sont définies :
2.
3.
4.
5.
6.
7.
alpha <- 0.15
beta <- 4
t1 <- 10
t2 <- 30
c1 <- 1000
c2 <- 3000
Q <- 4000
Puis les fonctions :
- f1 est la différence entre les temps de trajets sur les deux routes (quantité à minimiser) ;
- f2 est la dérivée de f1 ;
- f3 est la fonction utilisée pour mener à bien la méthode de Newton.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
f1 <- function (x) {
t1 * (1 + alpha * (x / c1) ^ beta) -
t2 * (1 + alpha * ((Q - x) / c2) ^ beta)
}
f2 <- function (xx) {
eval({x <- xx;
(D(expression(
t1 * ( 1 + alpha * (x / c1) ^ beta) -
t2 * (1 + alpha * ((Q - x) / c2) ^ beta)),
"x"))
})
}
f3 <- function(x) {
x - f1(x) / f2(x)
}
Une fois définies les constantes et les fonctions, la résolution numérique peut commencer. On décide arbitrairement d'une première estimation du nombre de voitures qui emprunteront la route 1 à l'équilibre, par exemple 1000 véhicules. On calcule x1 selon la méthode de Newton à partir de cette première estimation, puis x2, et ainsi de suite. L'algorithme ci-dessous calcule ainsi les dix premiers termes de cette suite.
2.
3.
4.
5.
seqConv <- NULL
seqConv[ 1] <- 1000
for(i in 2: 10) {
seqConv[i] <- f3(seqConv[i - 1])
}
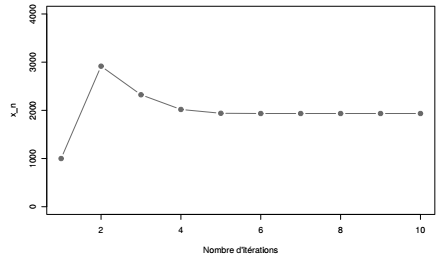
On peut ainsi représenter la convergence de cette suite vers le trafic à l'équilibre et reporter le temps de trajet dans cette configuration.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. |
|
|
|
Sélectionnez 1. 2. 3. 4. |
Dans cet exemple, la valeur qui satisfait l'équilibre de Wardrop est de 2000 véhicules sur chacune des deux routes.
III-C-4. Calcul des vols de Syracuse▲
Pour poursuivre l'apprentissage des fonctions et des tests conditionnels, cet exemple s'intéresse à une suite mathématique : la suite de Syracuse(11). Partant d'un nombre quelconque, à chaque itération, le nombre suivant vaut :
- la moitié du nombre si celui-ci est pair ;
- le triple du nombre augmenté de 1 si celui-ci est impair.
Autrement dit, à partir d'un entier non nul u 0, on définit la suite un par :
kitxmlcodelatexdvp\left\{\begin{matrix} u_{n+1} = & \frac{u_n}{2}\ si\ u_n\ pair \\ u_{n+1} = & 3u_n+1\ si\ u_n\ impair \end{matrix}\right.finkitxmlcodelatexdvpIl semble, bien que personne ne l'ait démontré, que quelle que soit la valeur de l'entier de départ, au bout d'un certain nombre d'itérations, on finit toujours par tomber sur 1. C'est ce que les fonctions suivantes vont permettre de vérifier empiriquement sur un certain nombre de cas.
Pour cela, on crée un vecteur qu'on initialise ensuite avec une valeur donnée. À l'aide d'une boucle while, on complète les valeurs de la suite. Il faut tester à chaque itération si le nombre est pair ou impair (avec la fonction %% qui renvoie le modulo) et, selon le résultat de ce test, calculer la valeur suivante.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
Syracuse <- function(nbr) {
seqSyr <- nbr
i <- 1
while (seqSyr[i] != 1) {
if (seqSyr[i] %% 2 == 0) {
seqSyr[i + 1] <- seqSyr[i] / 2
}
else {
seqSyr[i + 1] <- 3 * seqSyr[i] + 1
}
i <- i + 1
}
return(seqSyr)
}
Une seconde fonction est créée qui renvoie la longueur de la suite, c'est-à-dire le nombre d'itérations nécessaires pour converger vers 1. Ce nombre est qualifié de « durée du vol du Syracuse ».
SyracuseDuration <- function(x, fct) {
length(fct(x))
}Entrées et sorties des fonctions : à la création d'une fonction, tous les arguments spécifiés entre parenthèses sont les entrées de la fonction. Si un objet (données ou fonctions) n'est pas spécifié dans les arguments, R va le chercher dans l'environnement global. Quant aux sorties, R renvoie par défaut le dernier objet calculé par la fonction (voir la fonction SyracuseDuration). Si l'utilisateur souhaite être plus explicite ou renvoyer plusieurs objets en sortie, il peut utiliser la fonction return() (voir la fonction Syracuse).
Une fonction doit être, autant que possible, générique et sûre pour l'utilisateur. L'une des règles d'or dans l'écriture de fonctions est d'éviter ce qui a été fait plus haut avec les fonctions f1(), f2() et f3() : faire appel à des variables globales, c'est-à-dire des objets existant dans l'environnement global et non spécifiés dans les arguments de la fonction.
Pour approfondir ce sujet, il existe d'excellentes ressources, en anglais le livre en ligne d'Hadley Wickham(12), en français les manuels en ligne de Christophe Genolini(13).
Par exemple, la fonction f1() fait appel à plusieurs variables - alpha, beta, t1, t2, etc. - qui sont définies en dehors de la fonction. La fonction ainsi écrite n'est pas générique et elle peut être source d'erreurs. Elle aurait plutôt dû s'écrire de la façon suivante :
2.
3.
4.
f1 <- function (x, alpha, beta, c1, c2, t1, t2, Q) {
t1 * (1 + alpha * (x / c1) ^ beta) -
t2 * (1 + alpha * ((Q - x) / c2) ^ beta)
}
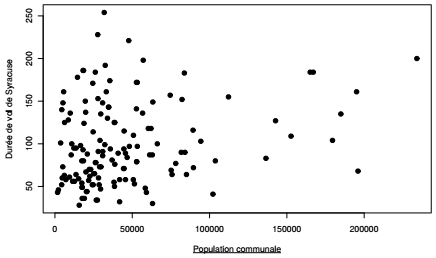
La durée des vols de Syracuse peut être calculée, grâce à la fonction définie précédemment, à partir d'un ensemble de valeurs de départ. Dans cet exemple, les vols de Syracuse sont calculés à partir des populations des communes de Paris et de petite couronne en 2008. L'idée est de déterminer s'il y a un lien entre la valeur de départ et la durée de vol, puis d'afficher le vol de la commune pour laquelle la durée de vol est la plus longue. L'application d'une fonction à tous les éléments d'un vecteur ou d'une liste se fait grâce aux fonctions de type apply présentées dans la section suivante.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. |
|
|
Il n'y a apparemment pas de lien entre la valeur de départ et la durée de vol, d'ailleurs la durée la plus importante (254 itérations) est obtenue pour une commune d'importance moyenne : Châtenay-Malabry.
2.
3.
4.
5.
6.
7.
max(syrDur)
## [1] 254
popCom3608$LIBELLE[ which.max(syrDur)]
## [1] "CHATENAY-MALABRY"
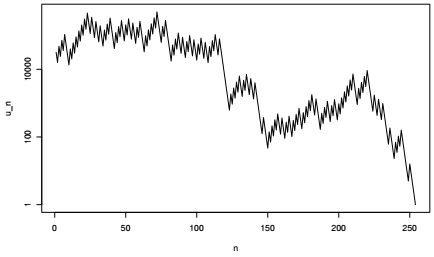
Et voici la représentation graphique du vol de Syracuse de la commune de Châtenay-Malabry.
|
Sélectionnez 1. 2. 3. 4. 5. |
|
|
Il est bien évident que l'application des durées de vol de Syracuse à des populations communales n'a pas d'autre sens que de jouer avec cette fonction mathématique et d'approfondir les techniques de création et de manipulation de fonctions avec R.
III-D. L'application de fonctions sur des ensembles▲
Le chapitre précédent a présenté certains traitements par blocs qui consistent à appliquer une fonction à un bloc de données (cf. Section 2.4.2Agrégations et traitements par blocs). Ces fonctions ont été exclusivement utilisées pour produire des résumés numériques sur des sous-groupes : tapply() ou aggregate() par exemple. Cette section présente de façon plus générale comment appliquer des fonctions à des ensembles avec la famille de fonctions apply(), sans qu'il s'agisse nécessairement de résumés numériques calculés selon une variable d'agrégation.
Ces fonctions sont inspirées du paradigme de la programmation fonctionnelle qui raisonne sur des ensembles. Elles sont très employées et remplacent avantageusement les boucles généralement plus lentes et plus gourmandes en ressources. L'exemple le plus simple consiste à calculer des moyennes ou des totaux marginaux sur un tableau. C'est le type de traitement que l'utilisateur d'un tableur fait fréquemment quand il entre une fonction en bout de ligne ou de colonne puis qu'il étire la fonction sur la dimension choisie.
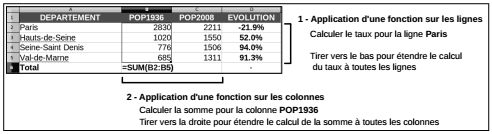
Pour faire ce type de calcul, par exemple calculer la somme de la population de la région d'étude à toutes les dates du recensement, une solution serait d'appliquer une boucle qui calcule successivement cette somme pour chaque colonne. L'utilisation de la fonction apply() sera dans ce cas bien meilleure, à la fois en lisibilité et en efficacité.
2.
3.
4.
5.
6.
7.
8.
9.
# Application de la fonction avec une boucle
sumPop <- vector()
for(i in 3: 11){
sumTemp <- sum(popCom3608[ , i])
sumPop <- append(sumPop, sumTemp)
}
# Application de la fonction avec apply
sumPop <- apply(popCom3608[ , 3: 11], 2, sum)
La syntaxe générale est la suivante :
apply(tableau, dimension(s), fonction)Les données attendues doivent être de type matrix ou array, s'il s'agit d'un data.frame l'objet est automatiquement transformé. Le deuxième argument est un entier désignant la dimension sur laquelle la fonction doit être appliquée : 1 pour les lignes et 2 pour les colonnes (s'il s'agit d'un tableau à deux dimensions). Il est aussi possible de travailler sur des matrices aux dimensions plus nombreuses, trois dimensions par exemple pour un cube de données. La fonction à appliquer peut être un résumé numérique simple comme c'est le cas ici, ou bien une fonction plus compliquée, créée par l'utilisateur si besoin.
Recherche d'efficacité : en termes de vitesse de calcul les boucles sont presque toujours plus mauvaises que les fonctions de la famille apply. De plus, le principe de la boucle, qui s'appuie à chaque itération sur les variables à l'état précédent, interdit toute tentative de calcul parallèle. Ceci est un des gros avantages des fonctions de la famille apply qui peuvent facilement être exécutées sur plusieurs processeurs avec des packages tels que parallel ou multicore.
Pour appliquer une fonction élément par élément sur un objet à une seule dimension, un vecteur ou une liste, la fonction à utiliser est lapply(). La syntaxe générale est la suivante :
lapply(liste, fonction)Par défaut le résultat renvoyé par lapply() est une liste. Il existe d'autres fonctions dérivées de lapply() qui renvoient d'autres types d'objets en sortie : sapply() et vapply() sont les plus courantes. C'est l'exemple présenté plus haut pour le calcul de la durée des vols de Syracuse (cf. Section 3.3.4Calcul des vols de Syracuse).
L'exemple présenté ci-dessous reprend les données historiques de la campagne de Russie des troupes de Napoléon. Ces données sont issues de la représentation cartographique de Charles Joseph Minard(14), considérée par certains comme le meilleur graphique jamais produit.
Les données sont mises à disposition dans le package HistData, elles contiennent les coordonnées des points constitutifs des segments de la carte, le nombre de survivants à chaque point, la direction (avancée ou retraite) ainsi que le groupe qui distingue : (1) l'armée principale, (2) le flanc gauche en direction de Polotsk et (3) le bataillon du Nord en direction de Riga.
library(HistData)
data(Minard.troops)L'idée est de calculer les pertes, en valeur absolue et relative, pour ces trois groupes. Dans un premier temps, le tableau est réorganisé dans une liste de trois éléments correspondant aux trois groupes de l'armée.
2.
3.
4.
5.
minardGroups <- list(
MAIN = Minard.troops$survivors[Minard.troops$group == 1],
LEFT = Minard.troops$survivors[Minard.troops$group == 2],
NORD = Minard.troops$survivors[Minard.troops$group == 3]
)
Dans un second temps, on construit une fonction qui, pour chaque élément de la liste, récupère le minimum et le maximum puis calcule la différence et le rapport entre le deux. Cette fonction est ensuite appliquée à la liste grâce à la fonction lapply() ou sapply().
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
Casualties <- function(vec){
absDif <- max(vec) - min(vec)
relDif <- round(absDif / max(vec), digits = 2)
return(list(ABS = absDif, REL = relDif))
}
# Sortie en format liste
casGroupsList <- lapply(minardGroups, Casualties)
# Sortie en format matrice
casGroupsMat <- sapply(minardGroups,
Casualties,
simplify = TRUE)
casGroupsMat
## MAIN LEFT NORD
## ABS 336000 32000 16000
## REL 0.99 0.53 0.73
Les pertes sont très différentes dans les trois groupes : le flanc gauche de l'armée n'a perdu « que » 53 % de son effectif alors que l'armée principale a été complètement décimée perdant 99 % de son effectif. Ce calcul aurait pu être effectué sur le tableau d'origine avec les fonctions des packages plyr et dplyr présentés dans le chapitre précédent.
Comme annoncé en introduction, il y a toujours différentes façons d'aboutir à un même résultat et chacun est libre de choisir celle qui lui convient le mieux. Dans ce choix, il faut savoir se frayer un chemin dans l'ensemble des solutions possibles et en choisir une qui soit lisible, pour soi-même et pour les autres, et qui soit efficace, surtout si le traitement est gourmand en puissance de calcul.
Au terme de ce chapitre, l'utilisateur sait utiliser les structures itératives et les tests conditionnels. Il comprend mieux l'objet fonction et il est capable de créer ses propres fonctions. Enfin, il sait appliquer ces fonctions à des blocs de données, ce qui lui confère une force de frappe importante pour attaquer des jeux de données de grande taille.