IV. CHAPITRE 4 Analyse univariée▲
Objectifs
Ce chapitre vise à présenter des manipulations simples nécessaires pour calculer des variables dérivées, réaliser des analyses univariées et afficher les représentations graphiques associées.
Prérequis
Valeurs centrales (moyenne, médiane) ; mesures de dispersion (variance, écart-type) ; discrétisation de variables continues ; représentations graphiques univariées.
Description des packages utilisés
La grande majorité des fonctions utilisées font partie des packages de base installés et chargés par défaut : le package base et le package stats. Seul un package supplémentaire sera utile ici : classInt développé par Roger Bivand, qui contient un ensemble de fonctions utiles pour la discrétisation de variables continues.
IV-A. Calculs simples et recodages▲
Les données utilisées sont les mêmes que dans les chapitres précédents, elles sont décrites à la Section 1.6L'exemple et les données.
2.
3.
4.
5.
6.
7.
socEco9907 <- read.csv("data/SocEco9907.csv",
sep = ";",
stringsAsFactors = FALSE)
popCom3608 <- read.csv("data/PopCom3608.csv",
sep = ";",
stringsAsFactors = FALSE)
Comme préalable aux manipulations présentées dans ce chapitre, plusieurs nouveaux champs sont calculés. Les variables suivantes sont créées : le taux d'évolution de la population entre 1936 et 2008 et la densité de population en 2008 ainsi que le taux d'emplois résidents en 2006 au niveau des communes et des arrondissements parisiens. Ce taux d'emploi est défini comme le rapport entre le nombre d'emplois localisés dans une commune et le nombre d'actifs résidant dans cette commune.
Deux nouvelles variables sont donc créées dans le tableau popCom3608 et une nouvelle variable dans le tableau socEco9907. Pour ce genre d'instructions, la fonction with() (cf. Section 2.1.5Désigner des lignes, des colonnes ou des valeurs) est utile pour éviter la répétition du tableau de référence.
2.
3.
4.
popCom3608$EVOLPOP <- with(popCom3608,
POP2008 / POP1936 - 1)
popCom3608$DENSITE <- with(popCom3608, POP2008 / SURF)
socEco9907$TXEMPL <- with(socEco9907, EMPLOI06 / ACTOCC06)
Deux nouvelles variables sont ensuite créées, qui seront utilisées par la suite pour analyser les configurations spatiales à Paris et en petite couronne : le département d'appartenance (CODDEP) et la distance à Paris (DISTCONT). La variable CODDEP est une extraction des deux premiers chiffres du code communal (CODGEO) produite avec la fonction substr() (cf. Section 2.4.2Agrégations et traitements par blocs) :
socEco9907$CODDEP <- substr(socEco9907$CODGEO, 1, 2)La variable Distance à Paris sera créée en deux temps : on calcule d'abord une variable continue de distance au centre de Paris en considérant que le 1er arrondissement est une approximation du centre géographique (barycentre) de Paris, puis on discrétise cette variable en quatre classes : < 5 km, 5-10 km, 10-15 km, > 15 km. Un rappel sur la formule de la distance euclidienne entre deux points i et j de coordonnées X et Y :
kitxmlcodelatexdvpD_{ij} = \sqrt{(X_i-X_j)^2+(Y_i-Y_j)^2}finkitxmlcodelatexdvpPour référencer les coordonnées géographiques du 1er arrondissement, deux solutions sont proposées : stocker ces coordonnées dans un vecteur à part (Option 1), ou bien faire une sélection à l'intérieur de la formule de calcul de la distance (Option 2), ce qui peut être effectué en indiquant les numéros de ligne et de colonne des coordonnées du 1er arrondissement ou en appelant les variables X et Y par exemple (cf. Section 2.1.5Désigner des lignes, des colonnes ou des valeurs). La distance obtenue est divisée par 10 pour obtenir une mesure en kilomètres parce que le système de projection est en hectomètres (plus de détails sur les systèmes de projection dans le Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie).
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
# Option 1
coordPremier <- as.numeric(socEco9907[ 1, 3: 4])
socEco9907$DISTCONT <- 0.1 * sqrt(
(socEco9907$X - coordPremier[ 1]) ** 2 +
(socEco9907$Y - coordPremier[ 2]) ** 2
)
# Option 2
socEco9907$DISTCONT <- 0.1 * sqrt(
(socEco9907$X - socEco9907[ 1, 3]) ** 2 +
(socEco9907$Y - socEco9907[ 1, 4]) ** 2
)
Maintenant, il ne reste plus qu'à discrétiser la variable continue DISTCONT dans une nouvelle variable DISTCLASS. Trois options sont proposées : la première est simple à comprendre, mais pas très efficace, elle consiste à assigner une valeur entre 1 et 4 en sélectionnant les cas où la condition est vérifiée. La deuxième est meilleure, elle consiste à emboîter une série de tests conditionnels avec la fonction ifelse(). La troisième option est sans doute la meilleure, elle consiste à créer la variable discrète avec la fonction cut() qui découpe une variable continue selon des seuils (breaks). Dans les trois cas, il est intéressant de vérifier avec la fonction class() le type de la variable créée : il s'agit d'un vecteur numérique dans les options 1 et 2 et d'un facteur dans l'option 3.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
# Option 1
socEco9907$DISTCLASS[socEco9907$DISTCONT < 5] <- 1
socEco9907$DISTCLASS[socEco9907$DISTCONT >= 5] <- 2
socEco9907$DISTCLASS[socEco9907$DISTCONT >= 10] <- 3
socEco9907$DISTCLASS[socEco9907$DISTCONT >= 15] <- 4
# Option 2
socEco9907$DISTCLASS <-
ifelse(socEco9907$DISTCONT < 5, 1,
ifelse(socEco9907$DISTCONT < 10, 2,
ifelse(socEco9907$DISTCONT < 15, 3, 4)))
# Option 3
breaksDist <- c(0, 5, 10, 15, max(socEco9907$DISTCONT))
socEco9907$DISTCLASS <- cut(socEco9907$DISTCONT,
breaks = breaksDist,
include.lowest = TRUE)
IV-B. Résumés statistiques▲
Quelques mesures de centralité et de dispersion sont calculées pour avoir un aperçu des distributions des variables utilisées. On peut calculer ces mesures au coup par coup : minimum, maximum, moyenne, médiane, écart-type, ou bien utiliser la fonction summary() qui renvoie toutes ces mesures sauf l'écart-type. Attention, il est nécessaire, mais non suffisant de calculer ces mesures : pour explorer correctement les variables, il faut les visualiser (sur l'importance de la visualisation, voir Section 5.2.1Représentation graphique de la relation).
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
min(popCom3608$EVOLPOP)
## [1] -0.5527
max(popCom3608$EVOLPOP)
## [1] 22.78
mean(popCom3608$EVOLPOP)
## [1] 1.851
median(popCom3608$EVOLPOP)
## [1] 0.6818
sd(popCom3608$EVOLPOP)
## [1] 3.15
summary(popCom3608$EVOLPOP)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## -0.553 0.193 0.682 1.850 2.190 22.800
Dans les packages de base, il y a peu de fonctions permettant de calculer des mesures pondérées ou de produire des tableaux de contingence pondérés. Ces fonctions sont implémentées dans le package Hmisc : wtd.mean(), wtd.table() ou encore wtd.quantile().
Ces fonctions sont particulièrement utiles pour qui travaille avec des données d'enquêtes issues d'un échantillon et dont les résultats sont assortis d'une variable de pondération. Dans le cadre d'un travail plus poussé sur ce type d'enquête, le package survey sera le plus indiqué : il permet bien sûr de calculer des mesures pondérées, mais il donne surtout tous les éléments pour traiter des enquêtes au design complexe.
Ici les variables ne sont pas pondérées, mais ces fonctions pourraient être utilisées pour calculer la proportion de cadres sur l'espace d'étude en 1999. Faire la moyenne des proportions de cadres par commune n'est pas satisfaisant puisque cela revient à attribuer un même poids à toutes les communes, quel que soit leur effectif de cadres.
À partir de la variable d'effectif de la population active occupée (ACTOCC99) et de la variable de proportion des cadres par commune (PCAD99), on peut calculer l'effectif total des cadres en multipliant les deux variables puis en sommant le résultat. Le rapport entre cette somme et la somme des actifs occupés donnera la proportion de cadres sur l'espace d'étude. Une solution plus rapide, qui ne demande pas la création d'une nouvelle variable, consiste à calculer la moyenne des proportions de cadres, pondérée par l'effectif de la population active occupée grâce à la fonction wtd.mean().
library(Hmisc)2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
# Option 1
socEco9907$NCAD99 <- with(socEco9907, PCAD99 * ACTOCC99)
sum(socEco9907$NCAD99) / sum(socEco9907$ACTOCC99)
## [1] 26.45
# Option 2
wtd.mean(socEco9907$PCAD99, weights = socEco9907$ACTOCC99)
## [1] 26.45
IV-C. Représentation graphique des distributions statistiques▲
Pour explorer correctement les variables, il faut les visualiser (voir l'exemple d'Anscombe, Section 5.2.1Représentation graphique de la relation). R propose un grand nombre de fonctions graphiques pour représenter graphiquement la distribution d'une variable. Il existe en outre plusieurs packages spécialisés dans les représentations graphiques, mais ici sont utilisées uniquement les fonctions du package graphics, installé et chargé par défaut. Le nom des fonctions est en général explicite quant au type de graphique créé : plot(), hist(), barplot(), boxplot(), etc.
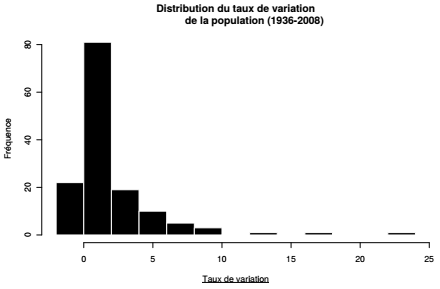
La fonction hist() renvoie par exemple l'histogramme de distribution d'une variable quantitative. Le graphique met en évidence une vingtaine de communes pour lesquelles le taux de variation est négatif, qui correspondent au vingt arrondissements parisiens plus quelques communes limitrophes.
|
Sélectionnez 1. 2. 3. 4. 5. 6. |
|
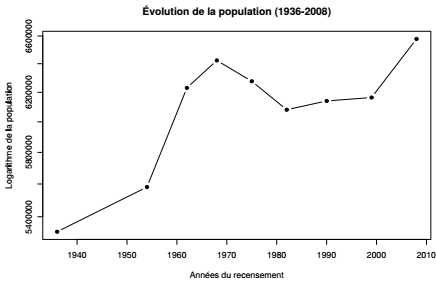
|
Il s'agit maintenant de calculer et visualiser l'évolution de la population depuis 1936 sur l'ensemble des 143 communes étudiées. Dans un premier temps, on somme les populations communales pour chacun des recensements de 1936 à 2008. Ceci peut être fait au coup par coup, pour chaque année, avec la fonction sum(), mais il est plus rapide d'utiliser la fonction apply() qui applique une fonction à l'ensemble d'une dimension d'un tableau (cf. Section 3.4L'application de fonctions sur des ensembles). Elle prend comme arguments l'ensemble de colonnes à considérer (ici les colonnes 3 à 11), la dimension sur laquelle appliquer la fonction (ici la dimension 2, qui indique les colonnes) et enfin la fonction à appliquer (ici la fonction sum()).
somPop3608 <- apply(popCom3608[, 3: 11], 2, sum)Concernant les dates des recensements, deux méthodes sont présentées : créer un vecteur en spécifiant chaque valeur et les combiner avec la fonction c(), ou bien extraire les dates des noms de colonnes de l'objet créé précédemment (somPop3608). Noter ici l'emboîtement de trois fonctions, names(), substr() et as.integer() : prendre les noms dans l'objet somPop3608, en extraire les caractères 4 à 7 et les transformer en entiers :
2.
3.
yearsLab <- c(1936, 1954, 1962, 1968, 1975,
1982, 1990, 1999, 2008)
yearsLab <- as.integer(substr(names(somPop3608), 4, 7))
Une fois créés ces deux vecteurs, on peut en faire la représentation graphique. Peu importe qu'il s'agisse de deux vecteurs distincts ou de deux champs appartenant au même tableau. Ici on précise plusieurs options, les titres du graphique et des axes, le type de représentation des valeurs (p pour points, l pour lines, b pour both), le fait que l'axe y est logarithmique et le type de point choisi (pch pour point character). On peut obtenir la liste des symboles ponctuels dans l'aide (?pch) :
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. |
|
|
On cherche maintenant à avoir des résumés de l'ensemble des variables renseignant sur la structure socioéconomique des communes en 2007 (de la variable TXCHOMA07 à la variable RFUCQ207). Cette requête est immédiate grâce à la fonction summary() appliquée à un ensemble de colonnes par la fonction apply(). Le résultat est un tableau que l'on transpose avec la fonction t() pour obtenir un rendu plus lisible :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
summaries07 <- apply(socEco9907[ , 25: 35], 2, summary)
t(summaries07)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## TXCHOMA07 6 8.0 10 11.50 14.0 23
## INTAO07 0 1.0 1 1.34 2.0 3
## PART07 2 4.0 4 4.88 5.5 11
## PCAD07 5 15.0 24 26.00 37.5 54
## PINT07 16 23.0 26 25.40 28.0 39
## PEMP07 15 22.0 30 28.60 35.0 43
## POUV07 3 8.5 14 15.10 21.5 37
## PRET07 8 13.0 15 15.20 17.0 21
## PMONO07 5 8.0 10 10.50 12.0 19
## PREFETR07 4 10.0 14 16.30 21.0 46
## RFUCQ207 9400 16100.0 20900 21700.00 26200.0 42900
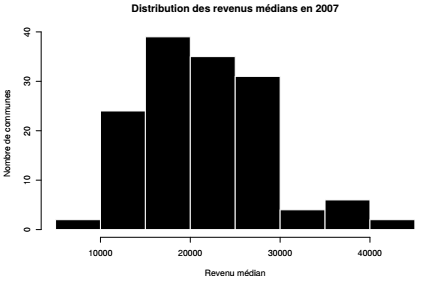
Finalement, on s'intéresse plus précisément à la distribution de la variable de revenus médians en 2007 :
|
Sélectionnez 1. 2. 3. 4. 5. 6. |
|
|
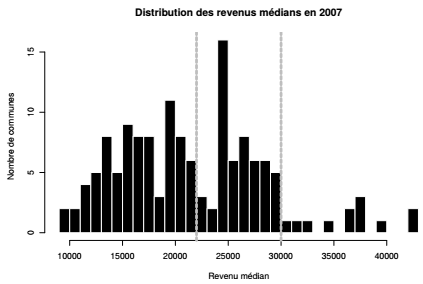
À partir de l'histogramme, on recode la variable de revenus médians en 2007 en trois classes pour préparer les analyses bivariées. La sortie par défaut de la fonction hist() n'indique aucun seuil qui permettrait de discrétiser la variable de façon pertinente. Si on force cette fonction à faire des barres plus fines (breaks) on observe une distribution trimodale, avec un seuil vers 22 000 € et un autre vers 30 000 €.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. |
|
|
On crée ensuite la variable discrétisée en découpant la variable continue selon les seuils observés dans l'histogramme précédent, grâce à la fonction cut() :
2.
3.
4.
5.
6.
7.
8.
breaksRev <- c(0, 22000, 30000, max(socEco9907$RFUCQ207))
socEco9907$REVCLASS <- cut(socEco9907$RFUCQ207,
breaks = breaksRev,
include.lowest = TRUE,
labels = c("[9000, 22000[",
"[22000, 30000[",
"[30000, 40000["))
À noter qu'il existe un package spécialisé dans la discrétisation nommé classInt. Il comprend des fonctions très utiles pour faire des cartes choroplèthes (cf. Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie) et ainsi retrouver les modes de discrétisation des logiciels classiques de cartographie. L'algorithme de Jenks utilisé ici crée des classes en minimisant la variance intraclasse et en maximisant la variance interclasse. L'objet créé par la fonction classIntervals() du package classInt est un objet spécifique de type classIntervals. Les seuils sont contenus dans un attribut breaks utilisé pour discrétiser comme précédemment. Au passage on note que ces seuils sont comparables à ceux fixés avec la méthode visuelle, à partir de l'histogramme.
library(classInt)2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
discretJenks <- classIntervals(var = socEco9907$RFUCQ207,
n = 3,
style = "jenks")
discretJenks$brks
## [1] 9404 20334 30274 42923
breaksJenks <- discretJenks$brks
socEco9907$RFUCQ207CLASSJENKS <- cut(socEco9907$RFUCQ207,
breaks = breaksJenks,
include.lowest = TRUE)
Au terme de ce chapitre, l'utilisateur dispose des principales fonctions de statistique univariée pour explorer ses données : calculer des mesures de centralité (moyenne, médiane), des mesures de dispersion (variance, écart-type) et produire des graphiques simples, en particulier des histogrammes. Ces résumés statistiques, ces représentations graphiques et ces nouvelles variables calculées ou recodées permettent maintenant d'aborder les analyses bivariées.