Partie 7 Données pondérées▲
S'il est tout à fait possible de travailler avec des données pondérées sous R, cette fonctionnalité n'est pas aussi bien intégrée que dans la plupart des autres logiciels de traitement statistique. En particulier, il y a plusieurs manières possibles de gérer la pondération.
Dans ce qui suit, on utilisera le jeu de données tiré de l'enquête Histoire de vie et notamment sa variable de pondération poids(28).
2.
3.
4.
R> data(hdv2003)
R> d <- hdv2003
R> range(d$poids)
[1] 78.07834 31092.14132
Options de certaines fonctions▲
Tout d'abord, certaines fonctions de R acceptent en argument un vecteur permettant de pondérer les observations (l'option est en général nommée weights ou row.w). C'est le cas, par exemple des méthodes d'estimation de modèles linéaires (lm) ou de modèles linéaires généralisés (glm), ou dans les analyses de correspondances des extensions ade4 (dudi.acm) ou FactoMineR (MCA).
Par contre, cette option n'est pas présente dans les fonctions de base comme mean, var, table ou chisq.test.
Fonctions de l'extension rgrs▲
L'extension rgrs propose quelques fonctions permettant de calculer des statistiques simples pondérées(29) :
- wtd.mean moyenne pondérée ;
- wtd.var variance pondérée ;
- wtd.table tris à plat et tris croisés pondérés.
On les utilise de la manière suivante :
2.
3.
4.
5.
6.
R> mean(d$age)
[1] 48.157
R> wtd.mean(d$age, weights = d$poids)
[1] 46.34726
R> wtd.var(d$age, weights = d$poids)
[1] 325.2658
Pour les tris à plat, on utilise la fonction wtd.table à laquelle on passe la variable en paramètre :
2.
3.
R> wtd.table(d$sexe, weights = d$poids)
Homme Femme
5149382 5921844
Pour un tri croisé, il suffit de passer deux variables en paramètres :
2.
3.
4.
R> wtd.table(d$sexe, d$hard.rock, weights = d$poids)
Non Oui
Homme 5109366.41 40016.02
Femme 5872596.42 49247.49
Ces fonctions admettent les deux options suivantes :
- na.rm si
TRUE, on ne conserve que les observations sans valeur manquante ; - normwt si
TRUE, on normalise les poids pour que les effectifs totaux pondérés soient les mêmes que les effectifs initiaux. Il faut utiliser cette option, notamment si on souhaite appliquer un test sensible aux effectifs comme le kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp.
Ces fonctions rendent possibles l'utilisation des statistiques descriptives les plus simples et le traitement des tableaux croisés (les fonctions lprop, cprop ou chisq.test peuvent être appliquées au résultat d'un wtd.table), mais restent limitées en termes de tests statistiques ou de graphiques…
L'extension survey▲
L'extension survey est spécialement dédiée au traitement d'enquêtes ayant des techniques d'échantillonnage et de pondération potentiellement très complexes. L'extension s'installe comme la plupart des autres :
R> install.packages("survey", dep = TRUE)Le site officiel (en anglais) comporte beaucoup d'informations, mais pas forcément très accessibles :
Pour utiliser les fonctionnalités de l'extension, on doit d'abord définir un design de notre enquête.
C'est-à-dire indiquer quel type de pondération nous souhaitons lui appliquer. Dans notre cas nous utilisons le design le plus simple, avec une variable de pondération déjà calculée. Ceci se fait à l'aide de la fonction svydesign :
R> library(survey)
R> dw <- svydesign(ids = ~1, data = d, weights = ~d$poids)Cette fonction crée un nouvel objet, que nous avons nommé dw. Cet objet n'est pas à proprement parler un tableau de données, mais plutôt un tableau de données plus une méthode de pondération. dw et d sont des objets distincts, les opérations effectuées sur l'un n'ont pas d'influence sur l'autre. On peut cependant retrouver le contenu de d depuis dw en utilisant dw$variables :
2.
3.
4.
R> mean(d$age)
[1] 48.157
R> mean(dw$variables$age)
[1] 48.157
Lorsque notre design est déclaré, on peut lui appliquer une série de fonctions permettant d'effectuer diverses opérations statistiques en tenant compte de la pondération. On citera notamment :
- svymean, svyvar, svytotal statistiques univariées ;
- svytable tableaux croisés ;
- svyglm modèles linéaires généralisés ;
- svyplot, svyhist, svyboxplot fonctions graphiques.
D'autres fonctions sont disponibles, comme svyratio ou svyby, mais elles ne seront pas abordées ici.
Pour ne rien arranger, ces fonctions prennent leurs arguments sous forme de formules, c'est-à-dire pas de la manière habituelle. En général l'appel de fonction se fait en spécifiant d'abord les variables d'intérêt sous forme de formule, puis l'objet design.
Voyons tout de suite quelques exemples :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
R> svymean(~age, dw)
mean SE
age 46.347 0.5284
R> svyvar(~heures.tv, dw, na.rm = TRUE)
variance SE
heures.tv 2.9886 0.1836
R> svytable(~sexe, dw)
sexe
Homme Femme
5149382 5921844
R> svytable(~sexe + clso, dw)
clso
sexe Oui Non Ne sait pas
Homme 2658744.04 2418187.64 72450.75
Femme 2602031.76 3242389.36 77422.79
En particulier, les tris à plat se déclarent en passant comme argument le nom de la variable précédé d'un symbole ~, tandis que les tableaux croisés utilisent les noms des deux variables séparés par un + et précédés par un ~.
On peut récupérer le tableau issu de svytable dans un objet et le réutiliser ensuite comme n'importe quel tableau croisé :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
R> tab <- svytable(~sexe + clso, dw)
R> tab
clso
sexe Oui Non Ne sait pas
Homme 2658744.04 2418187.64 72450.75
Femme 2602031.76 3242389.36 77422.79
R> lprop(tab)
clso
sexe Oui Non Ne sait pas Total
Homme 51.6 47.0 1.4 100.0
Femme 43.9 54.8 1.3 100.0
Ensemble 47.5 51.1 1.4 100.0
R> chisq.test(tab)
Pearson's Chi-squared test
data: tab
X-squared = 67214.28, df = 2, p-value < 2.2e-16
Les fonctions lprop, cprop et residus de rgrs sont donc tout à fait compatibles avec l'utilisation de survey. La fonction freq peut également être utilisée si on lui passe en argument non pas la variable elle-même, mais son tri à plat obtenu avec svytable :
2.
3.
4.
5.
6.
R> tab <- svytable(~peche.chasse, dw)
R> freq(tab, total = TRUE)
n %
Non 9716683 87.8
Oui 1354544 12.2
Total 11071226 100.0
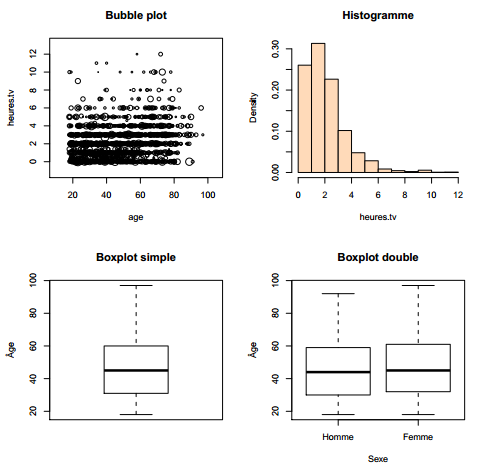
Enfin, survey est également capable de produire des graphiques à partir des données pondérées. Des exemples sont donnés figure 7.1.
Conclusion▲
En attendant mieux, la gestion de la pondération sous R n'est sans doute pas ce qui se fait de plus pratique et de plus simple. On pourra quand même donner les conseils suivants :
- utiliser les options de pondération des fonctions usuelles ou les fonctions de l'extension rgrs pour les cas les plus simples ;
- si on utilise survey, effectuer tous les recodages et manipulations sur les données non pondérées autant que possible ;
- une fois les recodages effectués, on déclare le design et on fait les analyses en tenant compte de la pondération ;
- surtout ne jamais modifier les variables du design. Toujours effectuer recodages et manipulations sur les données pondérées, puis redéclarer le design pour que les mises à jour effectuées soient disponibles pour l'analyse.
2.
3.
4.
5.
R> par(mfrow = c(2, 2))
R> svyplot(~age + heures.tv, dw, col = "red", main = "Bubble plot")
R> svyhist(~heures.tv, dw, col = "peachpuff", main = "Histogramme")
R> svyboxplot(age ~ 1, dw, main = "Boxplot simple", ylab = "Âge")
R> svyboxplot(age ~ sexe, dw, main = "Boxplot double", ylab = "Âge", xlab = "Sexe")
 R pour les sociologues (et assimilés)
R pour les sociologues (et assimilés)