III. Troisième partie - Pour aller plus loin▲
La suite comprend les signatures, l'héritage et quelques autres concepts avancés. Si vous êtes vraiment novice en programmation objet, il est peut-être temps de faire une petite pause pour intégrer ce qui vient d'être présenté. Ce que nous venons de voir suffit largement à faire quelques petites classes. Vos difficultés vous permettront entre autres de mieux comprendre le pourquoi de ce qui va suivre….
III-A. Chapitre 8 - Méthodes utilisant plusieurs arguments▲
Nous avons fait notre premier objet. La suite est plus liée aux interactions entre les objets. Il est donc temps de définir nos deux autres objets. En premier lieu, Partition.
III-A-1. 8.1 Le problème▲
Ceci est un manuel. Nous n'allons donc pas définir partition et le cortège de méthodes qui accompagne chaque nouvelle classe mais simplement ce dont nous avons besoin :
> setClass (
+ Class="Partition",
+ representation= representation(
+ nbGroupes ="numeric",
+ part ="factor"
+ )
+ )
[1] "Partition"
> setMethod(f ="[",signature ="Partition",
+ definition = function(x, i, j, drop){
+ switch(EXPR =i,
+ "part"= { return(x@part) },
+ "nbGroupes"={ return(x@nbGroupes) },
+ stop("Cet attribut n'existe pas !")
+ )
+
+ }
+ )
[1] "["
> partCochin <- new(Class="Partition", nbGroupes =2,
+ part = factor( c("A","B","A","B"))
+ )
> partStAnne <- new(Class="Partition", nbGroupes =2,
+ part = factor( rep(c("A","B"), c(50 ,30)) )
+ )Nous supposerons de plus que part est toujours composé de lettres majuscules allant de A à LETTERS[nbGroupes] (il faudra bien préciser dans la documentation de cette classe que le nombre de groupes doit être inférieur à 26). Nous pouvons nous permettre une telle supposition en programmant initialize et part<- de manière à toujours vérifier que c'est le cas.
Nous avons donc un objet trajCochin de classe Trajectoires et un découpage de cet objet en un objet partCochin de classe Partition. Lorsque nous représentons trajCochin graphiquement, nous obtenons un faisceau de courbes multicolores. Maintenant que les trajectoires sont associées à des groupes, il serait intéressant de dessiner les courbes en donnant une couleur à chaque groupe. Pour cela, il va falloir définir une méthode plot qui prendra comme argument un objet Trajectoires plus un objet Partition. C'est possible grâce à l'utilisation de signature.
III-A-2. signature▲
La signature, nous l'avons déjà vu lors de la définition de nos premières méthodes section II.B.1setMethod, est le deuxième argument fourni à setMethod. Jusqu'à présent, nous utilisions des signatures simples constituées d'une seule classe. Dans setMethod(f="plot",signature="Trajectoires",definition=function), la signature est simplement "Trajectoires".
Pour avoir des fonctions dont le comportement dépend de plusieurs objets, il est possible de définir un vecteur signature comportant plusieurs classes. Ensuite, quand nous appelons une méthode, R cherche la signature qui lui correspond le mieux et applique la fonction correspondante. Un petit exemple s'impose. Nous allons définir une fonction essai :
> setGeneric("essai", function(x,y ,...) { standardGeneric("essai") })
[1] "essai"Cette fonction a pour mission d'adopter un certain comportement si son argument est numeric, un autre comportement si s'est un character.
> setMethod(
+ f ="essai",
+ signature ="numeric",
+ function(x,y ,...) { cat("x est un numeric = ", x, "\n") }
+ )
[1] "essai"À ce stade, essai sait afficher les numeric, mais ne sait pas afficher les character :
> ### 3.17 étant un numeric , R va applique la methode
> ### essai pour les numeric
> essai(3.17)
x est un numeric = 3.17
> essai("E")
Error in function(classes, fdef, mtable) :
unable to find an
inherited method for function "essai", for signature "character"Pour qu'essai soit compatible avec les character, il faut définir la méthode avec la signature character :
> setMethod(
+ f ="essai",
+ signature ="character",
+ function(x,y ,...) { cat("x est character = ", x, "\n") }
+ )
[1] "essai"
> ### 'E' étant un character , R applique maintenant la méthode
> ### essai pour les characters
> essai("E")
x est character = EPlus compliqué, nous souhaitons que essai ait un comportement différent si on combine un numeric et un character.
> ### Pour une méthode qui combine numeric et character :
> setMethod(
+ f ="essai",
+ signature =c(x="numeric", y="character"),
+ definition = function(x,y ,...) {
+ cat(" Plus compliqué :")
+ cat("x est un num =", x, " ET y un est un char =", y, "\n")
+ }
+ )
[1] "essai"Maintenant, R connaît trois méthodes à appliquer à essai : la première est appliquée si l'argument de essai est un numeric ; la deuxième est appliquée si l'argument de essai est un character ; la troisième est appliquée si essai a deux arguments, un numeric puis un character
> essai(3.2, "E")
Plus compliqué :x est un num = 3.2 ET y un est un char = E
> essai(3.2)
x est un numeric = 3.2
> essai("E")
x est character = ERetour à miniKml (le package que nous sommes en train de construire). De la même manière, nous avions défini plot pour la signature Trajectoires, nous allons maintenant définir plot pour la signature c("Trajectoires", "Partition"). Nous pourrons ensuite représenter graphiquement les trajectoires selon des partitions spécifiques.
> setMethod(
+ f ="plot",
+ signature =c(x="Trajectoires", y="Partition"),
+ definition = function(x,y ,...) {
+ matplot(x@temps, t(x@traj[y@part=="A",]),
+ ylim = range(x@traj, na.rm=TRUE),
+ xaxt ="n", type ="l", ylab ="", xlab ="", col =2
+ )
+ for(i in 2: y@nbGroupes){
+ matlines(x@temps, t(x@traj[y@part == LETTERS[i],]),
+ xaxt ="n", type ="l", col=i+1
+ )
+ }
+ axis(1, at= x@temps)
+ }
+ )
[1] "plot"
> ### Plot pour 'Trajectoire'
> plot(trajCochin)
> plot(trajStAnne)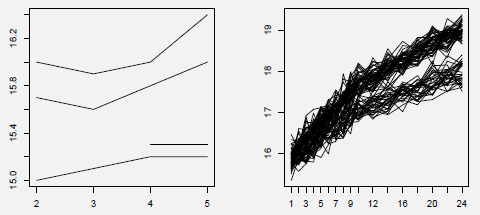
> ### Plot pour 'Trajectoire' et 'Partition'
> plot(trajCochin, partCochin)
> plot(trajStAnne, partStAnne)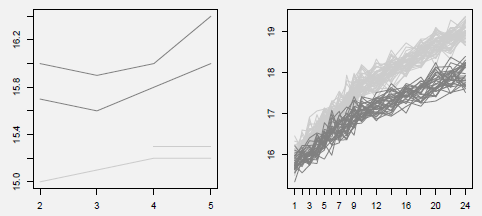
Plutôt élégant, n'est-il pas ?
III-A-3. missing▲
Il est également possible de définir une méthode ayant un certain comportement si elle a un unique argument, un autre comportement si elle en a plusieurs. Cela est possible grâce à missing. missing est vrai si l'argument est manquant :
> setMethod(
+ f ="essai",
+ signature =c(x="numeric", y="missing"),
+ definition = function(x,y ,...){
+ cat("x est numeric = ", x, " et y est 'missing'\n")
+ }
+ )
[1] "essai"
> ### Méthode sans y donc utilisant le missing
> essai(3.17)
x est numeric = 3.17 et y est 'missing'
> ### Methode avec y = 'character'
> essai(3.17, "E")
Plus compliqué :x est un num = 3.17 ET y un est un char = EIII-A-4. Nombre d'arguments d'une signature▲
Sans entrer dans les méandres internes de R, quelques petites règles concernant les signatures : une signature doit comporter autant d'arguments que sa méthode générique, ni plus, ni moins. Cela signifie qu'il n'est pas possible de définir une méthode pour print, qui prendra en compte deux arguments, puisque print a pour signature x. De même, plot ne peut être défini que pour deux arguments, impossible d'en préciser un troisième dans la signature.
III-A-5. ANY▲
Réciproquement, la signature doit comporter tous les arguments. Jusqu'à présent, nous ne nous en sommes pas souciés et nous avons défini des plot avec un seul argument. C'est simplement une facilité d'écriture : R est passé dernière nous et a ajouté le deuxième argument. Comme nous n'avions pas précisé le type de ce deuxième argument, il en a conclu que la méthode devait s'appliquer, quel que soit le type du deuxième argument.
Pour le déclarer explicitement, il existe un argument spécial, la classe originelle, la cause première : ANY (plus de détail sur ANY section III.B.2Père, grand-père et ANY). Donc, quand nous omettons un argument, R lui donne pour nom ANY.
La fonction showMethods, la même qui nous permettait de voir toutes les méthodes existantes pour un objet section II.B.4Voir les méthodes, permet d'afficher la liste des signatures que R connaît pour une certaine méthode :
> showMethods(essai)
Function : essai (package .GlobalEnv)
x="character", y="ANY"
x="numeric", y="ANY"
x="numeric", y="character"
x="numeric", y="missing"Comme vous pouvez le constater, la liste ne contient pas les signatures que nous avons définies, mais des signatures complétées : les arguments que nous n'avions pas précisés (à savoir y dans les cas x="character" et x="numeric") ont été remplacés par "ANY".
Plus précisément, ANY n'est utilisé que si aucun argument autre ne convient. Dans le cas de essai, si x est un numeric, R hésite entre trois méthodes. En premier lieu, il essaie de voir si y a un type défini par ailleurs. Si y est un character, la méthode utilisée sera celle correspondant à (x="numeric",y="character"). Si y n'est pas un character, R ne trouve pas de correspondance exacte entre y et un type, il utilise donc la méthode fourre-tout : x="numeric", y="ANY".
III-B. Chapitre 9 - Héritage▲
L'héritage est l'un des concepts clefs de la programmation objet. Il permet de réutiliser des pans entiers de programme à peu de frais. Dans notre cas, nous devons maintenant définir TrajDecoupees. Il va nous falloir coder l'objet, les constructeurs, les setteurs et les getteurs, l'affichage… Tout. Les plus astucieux d'entre nous sont déjà en train de se dire qu'il suffira de faire un copier-coller de méthodes créées pour Trajectoires et de les adapter. La programmation objet permet de faire mieux : nous allons définir TrajDecoupees comme objet héritier de Trajectoires.
III-B-1. Principe▲
L'héritage est un principe de programmation permettant de créer une nouvelle classe à partir d'une classe déjà existante, la nouvelle classe étant une spécialisation de la précédente. On dit de la nouvelle classe qu'elle hérite de la classe à partir de laquelle elle est définie. La nouvelle classe s'appelle donc classe fils alors que la classe ayant servi à la création est la classe père.
Plus précisément, la classe fils est une spécialisation de la classe père dans le sens ou elle peut faire tout ce que fait la classe père plus de nouvelles choses. Prenons un exemple, classique en programmation objet. La classe Vehicule est définie comme comprenant un attribut vitesse et une méthode tempsDeParcours, une méthode qui permet de calculer le temps mis pour parcourir une certaine distance. C'est donc une classe assez générale comprenant tout type de véhicule, de la trottinette au pétrolier.
On souhaite maintenant définir la classe Voiture. Cette classe peut être considérée comme un véhicule particulier. On peut donc définir Voiture comme classe héritière de Vehicule. Un objet Voiture aura les mêmes atrributs et méthodes que Vehicule, plus des attributs et méthodes propres, comme NombreDePortes. Cet attribut fait sens pour une voiture, mais le ferait bien moins pour le concept de véhicule au sens large du terme (parce qu'il serait ridicule de parler de portes pour une trottinette).
Formellement, une classe Fils peut hériter d'une classe Pere quand Fils contient au moins tous les attributs de Pere (plus éventuellement d'autres). Le fait d'hériter rend toutes les méthodes de Pere disponibles pour Fils : chaque fois que l'on utilisera une méthode sur un objet de classe Fils, R cherchera si cette méthode existe. S'il ne la trouve pas dans la liste des méthodes spécifiques à Fils, il cherchera dans les méthodes de Pere. S'il la trouve, il l'appliquera. S'il ne la trouve pas, il cherchera dans les méthodes dont Pere hérite. Et ainsi de suite.
On représente le lien qui unit le père et le fils par une flèche allant du fils vers le père. Cela symbolise que lorsqu'une méthode n'est pas trouvée pour le fils, R « suit » la flèche et cherche dans les méthodes du père : classPere ← classFils ou encore :
| Vehicule ← Voiture |
On note classiquement le père à gauche du fils (ou au-dessus) puisqu'il est défini avant.
III-B-2. Père, grand-père et ANY▲
Nous venons de le voir, quand R ne trouve pas une méthode pour un objet, le principe de l'héritage lui demande de chercher parmi les méthodes du père. Le principe est récursif.
S'il ne trouve pas chez le père, il cherche chez le grand-père et ainsi de suite. Sur notre exemple, nous pourrions considérer une classe de voiture particulière, les voitures sportives.
| Vehicule ← Voiture ← Sportive |
Si R ne trouve pas une méthode pour Sportive, il cherche parmi celle de Voiture. S'il ne trouve pas dans Voiture, il cherche dans Vehicule et ainsi de suite. Se pose alors la question de l'origine, de l'ancêtre ultime, la racine des racines. Chez les hommes, c'est -selon certaines sources non vérifiées- Adam. Chez les objets, c'est ANY. ANY est la classe première, celle dont toutes les autres héritent. Une classe créée de toutes pièces, sans que le programmeur ne la définisse comme héritière à partir d'une autre (comme toutes celles que nous avons créées dans les chapitres précédents) et est considérée par R comme héritière de ANY. Donc, si une méthode n'est pas trouvée pour une classe Fils, elle sera cherchée dans la classe Pere, puis GrandPere et ainsi de suite. Si elle n'est pas trouvée parmi les ancêtres (ou si Fils n'a pas de père), elle sera cherchée dans la classe ANY. Si elle n'existe pas pour ANY, une erreur est affichée.
III-B-3. contains▲
Nous allons donc définir TrajDecoupees comme héritière de Trajectoires. Pour cela, on déclare l'objet en ajoutant l'argument contains suivi du nom de la classe père.
> setClass (
+ Class="TrajDecoupees",
+ representation= representation(listePartitions ="list"),
+ contains ="Trajectoires"
+ )
~~~~~ Trajectoires : initiateur ~~~~~
~~~~~ Trajectoires : initiateur ~~~~~
[1] "TrajDecoupees"
> tdPitie <- new("TrajDecoupees")
~~~~~ Trajectoires : initiateur ~~~~~III-B-4. unclass▲
TrajDecoupees contient donc tous les attributs de Trajectoires plus son attribut personnel listePartitions (attribut qui contiendra une liste de partition).
Pour l'instant, il n'est pas possible de le vérifier directement. En effet, si nous essayons de « voir » tdCochin, nous obtenons l'affichage d'un objet Trajectoires et non pas une TrajDecoupees
> tdPitie
*** Class Trajectoires, method Show ***
* Temps = numeric(0)
* Traj (limité à une matrice 10x10) =
* ... ...
******* Fin Show(trajectoires) *******Voilà qui appelle quelques commentaires : TrajDecoupees est un héritier de Trajectoires. À chaque fois qu'une fonction est appelée, R cherche cette fonction pour la signature TrajDecoupees. S'il ne trouve pas, il cherche la fonction pour la classe parent à savoir Trajectoires. S'il ne trouve pas, il cherche dans les fonctions de ANY, c'est-à-dire les fonctions par défaut.
Voir un objet se fait grâce à show. Comme à ce stade show n'existe pas pour TrajDecoupees, c'est show pour Trajectoires qui est appelé à la place. Taper tdPitie ne nous montre donc pas l'objet tel qu'il est réellement, mais via le prisme show pour Trajectoires. Il est donc urgent de définir une méthode show pour les TrajDecoupees.
Néanmoins, il serait intéressant de pouvoir jeter un œil à l'objet que nous venons de créer. On peut, pour cela, utiliser unclass qui fait comme si un objet avait pour classe ANY. unclass(tdPitie) va donc appeler la méthode show comme si tdPitie avait pour classe ANY et va donc utiliser la méthode show par défaut. Résultat, l'objet est affiché sans fioritures, certes, mais dans son intégralité.
> unclass(tdPitie)
<S4 Type Object>
attr(,"listePartitions")
list()
attr(,"temps")
numeric(0)
attr(,"traj")
<0 x 0 matrix>L'objet comporte donc effectivement les attributs de Trajectoires plus une liste.
III-B-5. Arbre d'héritage▲
Plusieurs classes peuvent hériter d'un même père. Finalement, la représentation graphique des liens unissant les classes donne un arbre (un arbre informatique, désolé pour les poètes qui espéraient un peu de verdure dans cet ouvrage) :
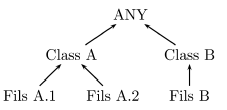
Il est théoriquement possible d'hériter de plusieurs pères. La représentation graphique n'est alors plus un arbre, mais un graphe. Mal utilisée, cette pratique peut être dangereuse. En effet, supposons qu'un objet B hérite à la fois de A1 et A2. Si une méthode n'existant pas pour B est appelée, elle sera recherchée dans les méthodes des pères. Si la méthode existe pour A1 ET pour A2, laquelle sera utilisée ? Celle de A1 ou celle de A2 ? Là réside une source de confusion. C'est encore plus problématique pour l'utilisation de callNextMethod (voir III.B.7callNextMethod).
Pourtant, dans certains cas, l'héritage multiple semble plein de bon sens. Prenons un exemple : la classe machineDeCalcul dispose de méthodes donnant la précision d'un calcul. La classe plastic précise les propriétés physiques du plastique, par exemple, ce qui se passe quand il brûle, sa résistance… Un ordinateur est à la fois une machineDeCalcul et outil en plastic. Il est donc intéressant qu'il accède à la fois à la méthode precision (pour savoir ce que l'on peut lui demander) et à la méthode brule pour savoir comment il réagira dans un incendie. La classe ordinateur pourrait donc légitimement hériter de deux pères.
Donc, l'héritage multiple est à manier avec précaution : il peut être utile, mais il faut prendre garde à ce qu'une classe n'hérite jamais de pères ayant des méthodes communes.
III-B-6. Voir la méthode en autorisant l'héritage▲
L'héritage est une force mais il peut être déroutant. Créons un deuxième objet TrajDecoupees :
> partCochin2 <- new("Partition", nbGroupes =3,
+ part = factor( c("A","C","C","B") )
+ )
> tdCochin <- new(
+ Class="TrajDecoupees",
+ temps =c(1 ,3 ,4 ,5),
+ traj = trajCochin@traj,
+ listePartitions = list(partCochin, partCochin2)
+ )
Error in .local(.Object, ...) :
argument(s) inutilisé(s)
(listePartitions = list (<S4 object of class "Partition">, <S4
object of class "Partition">))Ça ne marche pas… Pourquoi ? Pour le savoir, il est possible d'afficher la méthode initialize appelée par new :
> getMethod("initialize", "TrajDecoupees")
Error in getMethod("initialize", "TrajDecoupees") :
No method
found for function "initialize" and signature TrajDecoupeesLà encore, ça ne marche pas, mais cette fois la cause est plus simple à identifier : nous n'avons pas encore défini initialize pour Partition.
> existsMethod("initialize", "TrajDecoupees")
[1] FALSEVoilà la confirmation de nos doutes. Pourtant, R semble tout de même exécuter un code puisqu'il détecte une erreur. Mais que se passe-t-il donc(7) ? C'est un des effets indésirables de l'héritage, une sorte d'héritage involontaire.
En effet, à l'appel de new("TrajDecoupees"), new cherche la fonction initialize pour TrajDecoupees. Comme il ne la trouve pas ET que TrajDecoupees hérite de Trajectoires, il remplace la méthode manquante par initialize pour Trajectoires.
Pour vérifier cela, deux méthodes : hasMethods permet de savoir si une méthode existe pour une classe donnée en prenant en compte l'héritage. Pour mémoire, quand existsMethod ne trouvait pas une méthode, elle renvoyait faux. Quand hasMethod ne trouve pas, elle cherche chez le père, puis chez le grand-père et ainsi de suite :
> hasMethod("initialize", "TrajDecoupees")
[1] TRUEConfirmation, new ne repart pas bredouille, il est effectivement réorienté vers une méthode héritée. Pour afficher la méthode en question, on peut utiliser selectMethod qui a globalement le même comportement que getMethod. Seule différence, lorsqu'il ne trouve pas une méthode, il cherche chez les ancêtres… :
> selectMethod ("initialize", "TrajDecoupees")
Method Definition :
function(.Object, ...)
{
.local <- function(.Object, temps, traj)
{
cat(" ~~~~~ Trajectoires : initiateur ~~~~~\n")
if(!missing(traj)) {
colnames(traj) <- paste("T", temps, sep = "")
rownames(traj) <- paste("I", 1:nrow(traj), sep = "")
.Object@temps <- temps
.Object@traj <- traj
validObject(.Object)
}
return(.Object)
}
.local(.Object, ...)
}
Signatures :
.Object
target "TrajDecoupees"
defined "Trajectoires"Notre hypothèse était la bonne, TrajDecoupees utilise l'initiateur de Partition. Comme ce dernier ne connaît pas l'attribut listePartitions, il retourne une erreur. Le mystère est maintenant éclairci.
Pour pouvoir définir des objets TrajDecoupees un peu plus complexes, il faut donc au préalable définir initialize pour TrajDecoupees
> setMethod("initialize", "TrajDecoupees",
+ function(.Object, temps, traj, listePartitions){
+ cat(" ~~~~ TrajDecoupees : initiateur ~~~~\n")
+ if(!missing(traj)){
+ .Object@temps <- temps
+ # Affectation des attributs
+ .Object@traj <- traj
+ .Object@listePartitions <- listePartitions
+ }
+ # return de l'objet
+ return(.Object)
+ }
+ )
[1] "initialize"
> tdCochin <- new(
+ Class="TrajDecoupees",
+ traj = trajCochin@traj ,
+ temps =c(1, 3, 4, 5),
+ listePartitions = list(partCochin, partCochin2)
+ )
~~~~ TrajDecoupees : initiateur ~~~~Et voilà !
III-B-7. callNextMethod▲
Nous venons de le voir : lorsqu'il ne trouve pas une méthode, R dispose d'un mécanisme lui permettant de la remplacer par une méthode héritée. Il est possible de contrôler ce mécanisme et de forcer une méthode à appeler la méthode héritée. Ça permet, entre autres choses, de ré-utiliser du code sans avoir à le retaper. Cela se fait grâce à callNextMethod qui n'est utilisable que dans une méthode. Elle a pour effet d'appeler la méthode qui serait utilisée si la méthode actuelle n'existait pas. Par exemple, considérons la méthode print pour TrajDecoupees. Actuellement, cette méthode n'existe pas. Pourtant, un appel à print(tdCochin) serait quand même exécuté grâce à l'héritage :
> print(tdCochin)
*** Class Trajectoires, method Print ***
* Temps = [1] 1 3 4 5
* Traj =
[,1] [,2] [,3] [,4]
[1,] 15.0 15.1 15.2 15.2
[2,] 16.0 15.9 16.0 16.4
[3,] 15.2 NA 15.3 15.3
[4,] 15.7 15.6 15.8 16.0
******* Fin Print(trajectoires) *******Comme print n'existe pas pour TrajDecoupees, c'est print pour Trajectoires qui est appelée. Autrement dit, la nextMethod de print pour TrajDecoupees est print pour Trajectoires. Un petit exemple et tout sera plus clair. Nous allons définir print pour TrajDecoupees(8).
> setMethod(
+ f ="print",
+ signature ="TrajDecoupees",
+ definition = function(x ,...) {
+ callNextMethod()
+ cat("L'objet contient également ")
+ cat(length(x@listePartitions), "partition")
+ cat("\n***** Fin de print(TrajDecoupees) *****\n")
+ return(invisible())
+ }
+ )
[1] "print"
> print(tdCochin)
*** Class Trajectoires, method Print ***
* Temps = [1] 1 3 4 5
* Traj =
[,1] [,2] [,3] [,4]
[1,] 15.0 15.1 15.2 15.2
[2,] 16.0 15.9 16.0 16.4
[3,] 15.2 NA 15.3 15.3
[4,] 15.7 15.6 15.8 16.0
******* Fin Print(trajectoires) *******
L'objet contient également2 partition
***** Fin de print(TrajDecoupees) *****callNextMethod peut, soit prendre des arguments explicites, soit aucun argument. Dans ce cas, les arguments qui ont été passés à la méthode actuelle sont intégralement passés à la méthode suivante.
Quelle est la méthode suivante ? Voilà toute la difficulté et l'ambiguïté de callNextMethod. Dans la plupart des cas, les gens très forts savent, les moins forts ne savent pas. Mais là où cela devient totalement impropre, c'est que la méthode suivante peut dépendre de la structure d'une autre classe. Finalement, personne ne peut savoir. Exemple : définissons une classe A qui hérite de la classe B, classe que quelqu'un d'autre a programmée. Quelle est la méthode suivante de initialize pour A ? Cela dépend. Comme A hérite, R va chercher dans l'ordre :
- initialize pour B ;
- initialize par défaut. Cette méthode se termine par un validObject ;
- validObject pour A ;
- validObject pour B ;
- validObject par défaut.
À partir de là, il n'est pas possible de savoir, parce que ça ne dépend plus de nous ! Si le programmeur de B a défini un initialize, il est appelé et donc peut-être que le validObject pour B sera appelé, peut-être pas. Sinon, c'est le initialize par défaut qui est appelé, et donc le validObject pour A, celui de B ou celui par défaut en fonction de ce qui existe. Il est donc très difficile de savoir ce que le programme fait vraiment.
Plus grave, si le programmeur de B supprime ou ajoute un initialize, cela peut changer le comportement de notre méthode. Par exemple, si initialize pour B n'existe pas et que validObject pour A existe, initialize par défaut est appelé puis validObject pour A. Si la méthode initialize pour B est créée, initialize par défaut ne sera plus utilisé, mais surtout, il est probable que validObject ne sera plus utilisé non plus. Probable… Mais on ne sait pas vraiment.
Incertitude fortement désagréable, n'est-ce pas ? Voilà pourquoi l'utilisation de callNextMethod est à proscrire, surtout que as et is permettent de faire à peu près la même chose.
III-B-8. is, as et as<-▲
Quand un objet hérite d'un autre, on peut avoir besoin qu'il adopte momentanément le comportement qu'aurait son père. Pour cela, il est possible de le transformer en objet de la classe de son père grâce à as. Par exemple, si on veut imprimer tdPitie en ne considérant que son aspect Trajectoires :
> print( as(tdPitie, "Trajectoires") )
~~~~~ Trajectoires : initiateur ~~~~~
*** Class Trajectoires, method Print ***
* Temps = numeric(0)
* Traj =
<0 x 0 matrix>
******* Fin Print (trajectoires) *******Cela va nous servir dans la définition de show pour les TrajDecoupees :
> setMethod(
+ f ="show",
+ signature ="TrajDecoupees",
+ definition = function(object) {
+ show( as(object, "Trajectoires") )
+ lapply(object@listePartitions, show)
+ }
+ )
[1] "show"On peut vérifier qu'un objet est héritier d'un autre grâce à is qui vérifie que les attributs de l'objet sont présents dans la classe fils :
> is(trajCochin, "TrajDecoupees")
[1] FALSE
> is(tdCochin, "Trajectoires")
[1] TRUEEnfin, as<- permet de modifier uniquement les attributs qu'un objet hérite de son père. as(objetFils, "ClassPere")<-objetPere affecte le contenu des attributs objetPere aux attributs dont objetFils a hérité.
> ### Création d'un TrajDecoupees vide
> tdStAnne <- new("TrajDecoupees")
~~~~ TrajDecoupees : initiateur ~~~~
> ### Affectation d'un objet Trajectoires
> ### aux attributs d'un TrajDecoupees
> as(tdStAnne, "Trajectoires") <- trajStAnne
> tdStAnne
~~~~~ Trajectoires : initiateur ~~~~~
*** Class Trajectoires, method Show ***
* Temps = [1] 1 2 3 4 5 6 7 8 9 10 12 14 16 18 20 22 24
* Traj(limité à une matrice 10x10) =
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 16.25 16.1 16.16 16.53 16.67 17.2 17.55 17.3 17.47 17.55
[2,] 16.23 16.36 16.45 16.4 17.14 17 16.84 17.25 17.98 17.43
[3,] 15.89 16.02 16.15 16.69 16.77 16.62 17.52 17.26 17.46 17.6
[4,] 15.63 16.25 16.4 16.6 16.65 16.96 17.02 17.39 17.5 17.67
[5,] 16.16 15.85 15.97 16.32 16.73 16.94 16.73 16.98 17.64 17.72
[6,] 15.96 16.2 16.53 16.4 16.47 16.95 16.73 17.36 17.33 17.55
[7,] 16.03 16.33 16.23 16.67 16.79 17.14 17 17 .35 17.58 17.99
[8,] 15.69 16.06 16.63 16.72 16.81 17.16 16.98 17.41 17.51 17.43
[9,] 15.82 16.17 16.75 16.76 16.78 16.51 17.19 17.21 17.84 17.95
[10,] 15.98 15.76 16.1 16.54 16.78 16.89 17.22 17.18 16.94 17.36
* ... ...
******* Fin Show(trajectoires) *******III-B-9. setIs▲
En cas d'héritage, as et is sont définis « naturellement », comme nous venons de le voir. Il est également possible de les préciser « manuellement ». Par exemple, la classe TrajDecoupees contient une liste de Partitions. Elle n'hérite pas directement de Partition (ça serait un cas d'héritage multiple impropre), donc is et as ne sont pas définis par défaut.
Il est néanmoins possible de « forcer » les choses. Par exemple, on veut pouvoir considérer un objet de classe TrajDecoupees comme une Partition, celle ayant le plus grand nombre de groupes. Cela se fait avec l'instruction setIs qui est une méthode qui prend quatre arguments :
- from est la classe de l'objet initial, celui qui doit être transformé ;
- to est la classe en laquelle l'objet doit être transformé ;
- coerce est la fonction utilisée pour transformer from en to.
> setIs (
+ class1 ="TrajDecoupees",
+ class2 ="Partition",
+ coerce = function(from, to){
+ getNbGroupes <- function(partition) {
+ return( partition ["nbGroupes"])
+ }
+ nombreGroupes <-
+ sapply(from@listePartitions, getNbGroupes)
+ plusGrand <- which.max(nombreGroupes)
+ to <-new("Partition")
+ o@nbGroupes <-
+ from@listePartitions[[plusGrand]]["nbGroupes"]
+ to@part <- from@listePartitions[[plusGrand]]["part"]
+ return(to)
+ }
+ )
> as(tdCochin, "Partition")
An object of class "Partition"
Slot "nbGroupes":
[1] 3
Slot "part":
[1] A C C B
Levels : A B CÇa marche pour ce dont nous avions besoin. Mais un Warning apparaît. R nous annonce que as<- n'est pas défini. as<- est l'opérateur utilisé pour affecter une valeur à un objet alors qu'il est considéré comme un autre objet. Dans notre cas, as<- est l'opérateur utilisé pour modifier TrajDecoupees alors qu'elle est considérée comme une Trajectoires. Cela se fait grâce au quatrième argument de setIs :
- replace est la fonction utilisée pour les affectations.
Dans le cas présent, nous voudrions remplacer la partition ayant le plus grand nombre de groupes par une nouvelle :
> setIs(
+ class1 ="TrajDecoupees",
+ class2 ="Partition",
+ coerce = function(from, to){
+ getNbGroupes <- function(partition){
+ return(partition["nbGroupes"])
+ }
+ nombreGroupes <-
+ sapply(from@listePartitions, getNbGroupes)
+ plusGrand <- which.max(nombreGroupes)
+ to <-new("Partition")
+ to@nbGroupes <-
+ from@listePartitions[[plusGrand]]["nbGroupes"]
+ to@part <- from@listePartitions[[plusGrand]]["part"]
+ return(to)
+ },
+ replace = function(from, values){
+ getNbGroupes <- function(partition){
+ return(partition["nbGroupes"])
+ }
+ nombreGroupes <-
+ sapply(tdCochin@listePartitions, getNbGroupes)
+ plusGrand <- which.max(nombreGroupes)
+ from@listePartitions[[plusGrand]] <- values
+ return(from)
+ }
+ )
> as(tdCochin, "Partition") <- partCochin2Plus de Warning, la vie est belle.
Éventuellement, il est possible d'ajouter un cinquième argument, la fonction test : elle subordonne la transformation de class1 en class2 à une condition.
Nous venons d'expliquer à R comment considérer un objet TrajDecoupe comme une Partition. En réalité, un tel usage serait impropre, une TraDecoupees n'a pas à devenir une Partition. Si nous voulons accéder à une partition particulière, il nous faut définir un getteur (par exemple getPartitionMax).
De manière plus générale, setIs est une fonction à éviter. R convertit « naturellement » ce qui doit être converti. setIs ajoute des conversions artificielles au gré du programmeur, conversions qui seront peut-être « surprenantes » pour l'utilisateur. Et comme toujours, les surprises sont à proscrire.…
III-B-10. Les classes virtuelles▲
Il peut arriver que des classes soient proches sans que l'une soit une extension de l'autre. Par exemple, nous allons concevoir deux types de partitionnement : des découpages qui « étiquettent » les individus sans les juger et ceux qui évaluent les individus. Le premier type de découpage sera non ordonné (la même chose que Partition) et le second type sera ordonné (par exemple, il classera les individus en Insuffisant, Moyen, Bien). Les attributs de cette seconde classe seront nbGroupes, un entier qui indique le nombre de modalités de l'évaluation et part, une variable ordonnée qui indiquera le groupe d'appartenance. Clairement, les attributs ne sont pas les mêmes dans les deux classes puisque part est ordonné dans l'une et pas dans l'autre. Donc, l'une ne peut pas hériter de l'autre. Pourtant, les méthodes seront semblables dans bon nombre de cas.
Pour ne pas avoir à les programmer en double, on peut faire appel à une classe virtuelle. Une classe virtuelle est une classe pour laquelle il n'est pas possible de créer des objets mais qui peut avoir des héritiers. Les héritiers bénéficient ensuite des méthodes créées pour la classe. Dans notre cas, nous allons créer une classe virtuelle PartitionPere puis deux classes fils PartitionSimple et PartitionEvaluante. Toutes les méthodes communes seront créées pour PartitionPere, les deux fils en hériteront.
> setClass(
+ Class="PartitionPere",
+ representation= representation(nbGroupes ="numeric", "VIRTUAL")
+ )
[1] "PartitionPere"
> setClass(
+ Class="PartitionSimple",
+ representation= representation(part ="factor"),
+ contains ="PartitionPere"
+ )
[1] "PartitionSimple"
> setClass(
+ Class="PartitionEvaluante",
+ representation= representation(part ="ordered"),
+ contains ="PartitionPere"
+ )
[1] "PartitionEvaluante"
> setGeneric("nbMultDeux",
+ function(object){standardGeneric("nbMultDeux")}
+ )
[1] "nbMultDeux"
> setMethod("nbMultDeux", "PartitionPere",
+ function(object){
+ object@nbGroupes <- object@nbGroupes *2
+ return(object)
+ }
+ )
[1] "nbMultDeux"
> a <- new("PartitionSimple", nbGroupes =3,
+ part = factor(LETTERS[c(1 ,2 ,3 ,2 ,2 ,1)])
+ )
> nbMultDeux(a)
An object of class "PartitionSimple"
Slot "part":
[1] A B C B B A
Levels : A B C
Slot "nbGroupes":
[1] 6
> b <- new("PartitionEvaluante",nbGroupes =5,
+ part = ordered(LETTERS[c(1 ,5 ,3 ,4 ,2 ,4)])
+ )
> nbMultDeux(b)
An object of class "PartitionEvaluante"
Slot "part":
[1] A E C D B D
Levels : A < B < C < D < E
Slot "nbGroupes":
[1] 10Et voilà…
III-B-11. Pour les dyslexiques…▲
Pour conclure avec l'héritage, une petite astuce mnémotechnique destinée aux dyslexiques (dont moi) qui se mélangent assez vite les neurones et qui ne savent jamais si l'héritier peut utiliser les techniques du père ou si c'est l'inverse : l'histoire est issue de « Contes et légendes de la naissance de Rome » [3]. L'auteur explique que, contrairement aux humains les Dieux n'aiment pas avoir des enfants plus puissants qu'eux. C'est pour ça que Saturne dévore ses propres enfants à leur naissance (pour les émotifs, rassurez-vous, ça n'est tout de même pas trop grave pour les enfants puisque, lorsque Saturne se fait finalement couper en deux par son fils Jupiter, tous sortent de son ventre et sont bien vivants !). Chez les humains, c'est l'inverse, les pères sont plutôt fiers d'avoir des enfants plus grands, qui les battent au tennis (sur le moment ils râlent, mais après ils racontent à leurs copains), avec un meilleur niveau d'études…. C'est l'ascenseur social qui fonctionne. Chez les objets, c'est pareil que chez les humains : les fils sont plus forts que les pères. Un fils peut faire tout ce que fait le père, plus ce qui lui est propre(9).
III-C. Chapitre 10 - Modification interne d'un objet▲
La suite nécessite de descendre un peu plus profondément dans les méandres du fonctionnement de R…
III-C-1. Fonctionnement interne de R : les environnements▲
Un environnement est un espace de travail permettant de stocker des variables. Pour simplifier, R travaille en utilisant deux environnements : le global et le local. Le global est celui auquel nous avons accès quand nous tapons des instructions dans la console.
Le local est un environnement qui se crée à chaque appel de fonction. Puis, quand la fonction se termine, le local est détruit. Exemple :
> func <- function () {
+ x <- 5
+ cat(x)
+ return(invisible())
+ }
> ### Creation de x 'global'
> x <- 2
> cat(x)
2
> ### Appel de la fonction et création de x 'local'
> func()
5
> ### Retour au global , suppression de x local
> cat(x)
2La fonction func est définie dans l'environnement global. Toujours dans le global, x reçoit la valeur 2. Puis la fonction func est appelée. R crée donc l'environnement local. Dans le local, il donne à x la valeur 5. Mais uniquement dans le local. À ce stade, il existe donc deux x : un global qui vaut 2 et un local qui vaut 5.
La fonction affiche le x local puis se termine. L'environnement local est alors détruit. Ainsi, le x qui valait 5 disparaît. Reste le x qui vaut 2, le global.
III-C-2. Méthode pour modifier un attribut▲
Retour à nos trajectoires. Il nous reste une troisième méthode à définir, celle qui impute les variables. Pour simplifier, nous imputerons en remplaçant par la moyenne(10).
> meanSansNa <- function(x){ mean(x,na.rm=TRUE) }
> setGeneric("impute",function(object){standardGeneric("impute")})
[1] "impute"
> setMethod(
+ f ="impute",
+ signature ="Trajectoires",
+ def = function(object){
+ moyenne <- apply(object@traj, 2, meanSansNa)
+ for(iCol in 1:ncol(object@traj)){
+ object@traj[is.na(object@traj[,iCol]), iCol] <-
+ moyenne[iCol]
+ }
+ return(object)
+ }
+ )
[1] "impute"
> impute(trajCochin)
*** Class Trajectoires, method Show ***
* Temps = [1] 2 3 4 5
* Traj(limité à une matrice 10x10) =
[,1] [,2] [,3] [,4]
[1,] 15 15.1 15.2 15.2
[2,] 16 15.9 16 16.4
[3,] 15.2 15.53 15.3 15.3
[4,] 15.7 15.6 15.8 16
* ... ...
******* Fin Show(trajectoires) *******La méthode impute fonctionne correctement. Par contre, elle ne modifie pas trajCochin.
> trajCochin
*** Class Trajectoires, method Show ***
* Temps = [1] 2 3 4 5
* Traj (limité à une matrice 10x10) =
[,1] [,2] [,3] [,4]
[1,] 15 15.1 15.2 15.2
[2,] 16 15.9 16 16.4
[3,] 15.2 NA 15.3 15.3
[4,] 15.7 15.6 15.8 16
* ... ...
******* Fin Show(trajectoires) *******À la lumière de ce que nous venons de voir sur les environnements, que fait cette méthode ? Elle crée localement un objet object, elle modifie ses trajectoires (imputation par la moyenne) puis elle retourne un objet. Le fait d'avoir tapé impute(trajCochin) n'a donc eu aucun effet sur trajCochin.
Conceptuellement, c'est un problème. Bien sûr, il est facile de le contourner, simplement en utilisant :
> trajCochin <- impute(trajCochin)Mais impute est une fonction qui a pour vocation de modifier l'intérieur de l'objet, pas de créer un nouvel objet et de le réaffecter. Pour lui rendre son sens premier, nous pouvons utiliser assign.
assign est l'un des opérateurs les plus impropres qui soit.… Il permet, alors que l'on se trouve dans l'environnement local, de modifier des variables au niveau global. C'est très mal. Mais dans le cas présent, c'est justement ce que R ne nous offre pas, et qui est pourtant classique en programmation objet. Donc, nous nous permettons ici une petite entorse aux règles (ne le dites à personne, hein ?) en espérant qu'une prochaine version de R intègre la modification interne….
Nous allons donc réécrire impute en ajoutant deux petites instructions : deparse(substitute()) permet de connaître le nom de la variable qui, au niveau global, a été passée comme argument à la fonction en cours d'exécution.
assign permet de modifier une variable de niveau supérieur. Plus précisément, il n'existe pas « un » niveau local, mais « des » niveaux locaux. Par exemple, une fonction dans une autre fonction crée un local dans le local, une sorte de sous-local ou de local niveau 2. L'utilisation de assign que nous proposons ici n'affecte donc pas le niveau global, mais le niveau local supérieur. Modifier directement le global serait encore plus impropre….
> essaiCarre <- function(x){
+ nomObject <- deparse( substitute(x) )
+ print(nomObject)
+ assign(nomObject, x^2, envir = parent.frame())
+ return( invisible() )
+ }
> a <-2
> essaiCarre(a)
[1] "a"
> a
[1] 4Voilà donc impute nouvelle version. Pour l'utiliser, plus besoin de faire une affectation. Pour les Trajectoires, cela donne :
> setMethod(
+ f ="impute",
+ signature ="Trajectoires",
+ def = function(object){
+ nameObject <- deparse(substitute(object))
+ moyenne <- apply(object@traj, 2, meanSansNa)
+ for(iCol in 1: ncol(object@traj)){
+ object@traj[is.na(object@traj[,iCol]), iCol] <-
+ moyenne[iCol]
+ }
+ assign(nameObject, object, envir = parent.frame())
+ return( invisible() )
+ }
+ )
[1] "impute"
> impute(trajCochin)
> trajCochin
*** Class Trajectoires, method Show ***
* Temps = [1] 2 3 4 5
* Traj (limité à une matrice 10x10) =
[,1] [,2] [,3] [,4]
[1,] 15 15.1 15.2 15.2
[2,] 16 15.9 16 16.4
[3,] 15.2 15.53 15.3 15.3
[4,] 15.7 15.6 15.8 16
* ... ...
******* Fin Show(trajectoires) *******Ça marche. Encore une fois, assign est un opérateur impropre à manipuler avec beaucoup de précautions, il peut provoquer des catastrophes parfaitement contre-intuitives. Mais pour la modification interne il est, à ma connaissance, la seule solution.


