V. CHAPITRE 5 Analyse bivariée▲
Objectifs
Ce chapitre propose un ensemble de méthodes et de représentations graphiques de statistique bivariée appliquées à l'étude de données géographiques.
Prérequis
Analyse univariée, corrélation et régression linéaire, analyse de la variance, tests d'hypothèses.
Description des packages utilisés
Les packages de base installés et chargés par défaut suffisent pour les analyses proposées ici. Néanmoins, les packages spécialisés dans la représentation graphique, comme ggplot2 ou lattice, peuvent s'avérer très utiles pour représenter des relations bi- ou multivariées comme la répartition d'une distribution au sein des différentes modalités d'une variable qualitative.
V-A. Préambule▲
V-A-1. Types de variables▲
Les représentations graphiques et les méthodes d'analyse des relations entre deux variables diffèrent selon la nature des variables. Deux grands types sont distingués : les variables quantitatives, sur lesquelles des résumés numériques peuvent être calculés (âge pour des individus, population pour des communes) ; les variables qualitatives, qui regroupent les individus dans un nombre fini de modalités (sexe pour des individus, département d'appartenance pour des communes).
Il faut bien distinguer la nature de la variable de son format de stockage, numérique ou alphanumérique. Une variable qualitative peut être codée avec des caractères alphanumériques (Homme et Femme par exemple) aussi bien qu'avec des caractères numériques (0 et 1 par exemple, 0 signifiant Homme et 1 signifiant Femme). Une variable quantitative peut être codée avec des caractères numériques aussi bien qu'avec des caractères alphanumériques : soixante-deux, voire LXII pour 62.
L'analyse d'une relation bivariée avec deux types de variables possibles, quantitatif et qualitatif, se résume à trois cas : relation entre deux variables quantitatives (Section 5.2Relation entre deux variables quantitatives), relation entre une variable qualitative et une variable quantitative (Section 5.3Relation entre une variable quantitative et une variable qualitative) et relation entre deux variables qualitatives (cf. Section 5.4Relation entre deux variables qualitatives). Ces trois cas sont étudiés successivement : (1) relation entre la densité d'habitants au kilomètre carré en 2008 et la distance euclidienne au centre de Paris ; (2) relation entre le revenu par habitant en 2007 et les classes de distance à Paris ; (3) relation entre le résultat obtenu au référendum européen de 2005 et le département d'appartenance de la commune.
V-B. Relation entre deux variables quantitatives▲
Cet exemple s'intéresse à la relation entre la densité de population et la distance au centre de l'agglomération parisienne, centre défini de façon simple comme le centroïde du 1er arrondissement de Paris. Avant de commencer, on récupère certaines variables calculées dans le chapitre précédent.
dataCom <- merge(socEco9907, popCom3608, by = "CODGEO")V-B-1. Représentation graphique de la relation▲
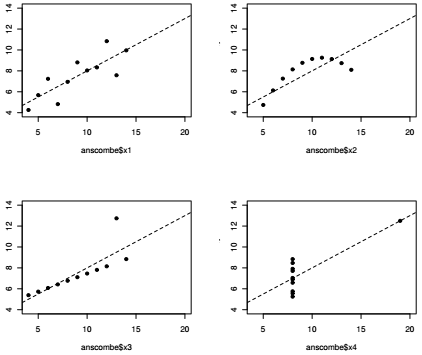
Aucune démarche s'appuyant sur des données empiriques ne peut se passer d'exploration. L'exploration des données s'appuie sur les mesures de centralité et de dispersion présentée dans le chapitre précédent, mais elle doit aussi utiliser les outils de visualisation graphique. C'est ce qu'a voulu montrer Francis Anscombe dans un exemple célèbre(15), repris par Edward Tufte dans son manuel de visualisation.
Anscombe propose quatre paires de variables x-y : prises une à une, ces variables ont les mêmes propriétés statistiques (moyenne, médiane, variance); prises deux à deux, les mesures de corrélation (coefficient de Pearson, droite de régression) sont également identiques. En revanche, la visualisation de ces relations écarte toute ressemblance entre ces quatre configurations.
Comme beaucoup de jeux de données historiques, les données d'Anscombe sont contenues dans R et peuvent être appelées avec la fonction data(). Pour produire le nuage de points, c'est la fonction plot() qui est utilisée. Il s'agit d'une fonction graphique générique (cf. Section 3.3.1Premier aperçu sur les fonctions), appliquée à deux variables quantitatives (vecteurs numériques), elle produit un nuage de points (scatterplot) : un individu statistique i est représenté par un point dont les coordonnées sont les valeurs xi et yi prises par les deux variables à l'étude.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. |
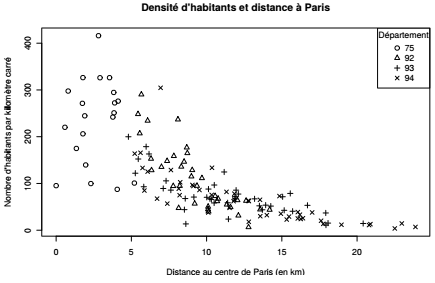
Dans le cadre d'une démarche exploratoire, il pourrait être intéressant de repérer les points en ajoutant le nom ou le code des communes, ou encore de différencier les départements d'appartenance par une variation de couleurs ou de symboles. La fonction text() permet d'ajouter un label aux points, la variation de couleurs peut être spécifiée avec l'argument col de la fonction plot() et la variation de symboles avec l'argument pch. C'est cette dernière option qui est utilisée ici pour des raisons de lisibilité sur un support papier en noir et blanc.
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. |
|
|
À la lecture du graphique, on retrouve les principes de la loi de Clark pour le cas parisien : la densité décroît avec la distance au centre selon une fonction exponentielle négative.
V-B-2. Calcul et significativité des corrélations▲
Afin de mesurer l'intensité des relations linéaires entre les variables quantitatives retenues pour l'analyse, il faut étudier les corrélations entre variables. Dans une démarche exploratoire, une telle analyse est particulièrement intéressante, car elle permet d'éviter de traiter, par la suite, des informations redondantes.
Avant d'analyser spécifiquement une relation, on a souvent besoin de calculer la matrice de corrélations entre un ensemble de variables. C'est ce que l'on propose de faire pour un ensemble de variables quantitatives décrivant les communes de la petite couronne et les arrondissements parisiens pour l'année 2007 que nous intégrons dans un nouveau tableau : le taux de chômage, la proportion de ménages dont la personne de référence est étrangère, le revenu médian communal, la densité et la distance au centre de l'agglomération. Ce nouveau tableau est ensuite donné comme argument de la fonction cor() qui calcule les corrélations entre toutes les variables. La méthode utilisée ici est celle de Pearson, mais l'argument method permet d'en utiliser d'autres. La méthode Spearman est adaptée pour analyser des relations non linéaires parce qu'elle ne travaille pas directement sur les valeurs prises par les variables, mais sur les rangs.
2.
3.
4.
5.
6.
7.
8.
9.
varCorr <- dataCom[, c(25, 34, 35, 39, 55)]
cor(varCorr, method = "pearson")
## TXCHOMA07 PREFETR07 RFUCQ207 DISTCONT EVOLPOP
## TXCHOMA07 1.0000 0.9201 -0.80343 -0.17094 -0.12933
## PREFETR07 0.9201 1.0000 -0.74938 -0.17607 -0.13228
## RFUCQ207 -0.8034 -0.7494 1.00000 -0.09421 -0.06114
## DISTCONT -0.1709 -0.1761 -0.09421 1.00000 0.61367
## EVOLPOP -0.1293 -0.1323 -0.06114 0.61367 1.00000
La matrice de corrélation proposée par la fonction cor() permet de connaître la valeur du coefficient de corrélation pour chaque couple de variables. La valeur de ce coefficient est bornée dans un intervalle compris entre − 1 et +1. Un coefficient négatif proche de − 1 indique une forte corrélation négative entre les variables : quand l'une augmente, l'autre a tendance à décroître. À l'inverse, un coefficient proche de +1 signifie qu'il existe une corrélation positive entre les variables, autrement dit que les deux variables ont tendance à croître ou à décroître conjointement. Enfin, un coefficient de corrélation proche de zéro décrit une absence de relation linéaire entre les deux variables.
Dans la matrice de corrélation ci-dessus, on remarque une forte corrélation linéaire positive entre le taux de chômage et la proportion de ménages dont la personne de référence est étrangère, les deux variables étant négativement corrélées au revenu médian de la commune. Le coefficient de corrélation entre la densité et la distance au centre est assez élevé (0,75).
Le nuage de points ci-dessus montre pourtant que la relation entre densité et distance au centre n'est pas linéaire. Pour étudier cette relation et tester sa significativité, deux options sont envisageables : la première consiste à utiliser une méthode qui ne requiert pas la linéarité de la relation ni la normalité des variables (Spearman); la seconde consiste à transformer la variable DENSITE avec une fonction logarithme. La variable ainsi transformée a une distribution presque normale et la relation devient linéaire. Ces deux options sont illustrées ici.
2.
3.
4.
5.
6.
7.
cor.test(dataCom$DISTCONT,
dataCom$DENSITE,
method = "spearman")
cor.test(dataCom$DISTCONT,
log(dataCom$DENSITE),
method = "pearson")
La fonction renvoie la valeur du coefficient de corrélation, les bornes de l'intervalle de confiance, la valeur du t de Student et la p-value. Ce test confirme la relation négative observée sur le nuage de points. La fonction cor.test() donne les éléments suivants en sortie : la statistique de test, le degré de liberté, la valeur de la probabilité critique (p-value), l'intervalle de confiance du coefficient et le coefficient de corrélation. La valeur de pest inférieure à 0.001, aussi, le coefficient de Pearson est statistiquement significatif (non nul). En outre, la valeur absolue du coefficient de Pearson est relativement élevée (−0, 85), ce qui indique une relation linéaire forte entre les deux variables. Le signe du coefficient renseigne, enfin, sur le fait que la relation est négative : lorsque la distance au centre de Paris augmente, la densité de population décroît.
V-B-3. Régression linéaire simple▲
La relation linéaire entre les deux variables quantitatives est modélisée avec la fonction lm() (linear model) qui permet de calculer des régressions linéaires simples et multiples. La variable à expliquer (dépendante) est la variable de densité, c'est elle que l'on cherche à expliquer statistiquement par la variable de distance, qui est la variable explicative ou indépendante. Ce modèle s'écrit de la façon suivante :
kitxmlcodelatexdvpy_i = b_0 + b_1x_i + \epsilon_ifinkitxmlcodelatexdvpLe nuage de points de la section précédente montre que la relation entre densité de population et distance au centre n'est pas linéaire, mais exponentielle. Dans ce cas, il est utile d'opérer une transformation semi-logarithmique : on modélisera le logarithme de la variable de densité. Le terme kitxmlcodeinlinelatexdvpy_ifinkitxmlcodeinlinelatexdvp est la densité de la commune kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpx_ifinkitxmlcodeinlinelatexdvp est la distance de cette commune au centre de l'agglomération. Les paramètres de la droite de régression sont notés kitxmlcodeinlinelatexdvpb_0finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpb_1finkitxmlcodeinlinelatexdvp, ils désignent respectivement l'intercept de la droite, c'est-à-dire la valeur prise par kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp lorsque kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp est égal à zéro, et sa pente, qui est le facteur constant qui lie kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp. Enfin, kitxmlcodeinlinelatexdvp\epsilon_ifinkitxmlcodeinlinelatexdvp est le terme d'erreur ou résidu pour la commune kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, c'est-à-dire la différence entre valeur observée et valeur modélisée de la variable kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp.
Transformation logarithmique : dans un modèle de régression linéaire simple, la transformation est dite logarithmique lorsque les deux variables kitxmlcodeinlinelatexdvpxfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpyfinkitxmlcodeinlinelatexdvp sont passées en logarithmes, elle est dite semi-logarithmique lorsque cette transformation n'est appliquée qu'à la variable à expliquer kitxmlcodeinlinelatexdvp(y)finkitxmlcodeinlinelatexdvp. Ici la relation entre densité kitxmlcodeinlinelatexdvp(y)finkitxmlcodeinlinelatexdvp et distance au centre kitxmlcodeinlinelatexdvp(x)finkitxmlcodeinlinelatexdvp est de type kitxmlcodeinlinelatexdvpy = \exp(ax)finkitxmlcodeinlinelatexdvp, la transformation semi-logarithmique donne ainsi une relation linéaire de type kitxmlcodeinlinelatexdvp\log(y) = axfinkitxmlcodeinlinelatexdvp.
La fonction lm() produit une liste d'éléments renseignant sur les estimations du modèle. La fonction names() liste les noms de ces différents résultats et la fonction summary() permet quant à elle de connaître les principaux résultats du modèle : résidus, coefficients et qualité de l'ajustement linéaire. Plus particulièrement, le tableau donne, pour chacun des deux paramètres du modèle kitxmlcodeinlinelatexdvpb_0finkitxmlcodeinlinelatexdvp (intercept) et kitxmlcodeinlinelatexdvpb_1finkitxmlcodeinlinelatexdvp (pente) :
- son estimation (colonne 1) ;
- l'estimation de son erreur standard (colonne 2) ;
- la valeur de la statistique du test de Student (colonne 3) ;
- la significativité du coefficient (valeur de p).
lmDensDist <- lm(log(DENSITE) ~ DISTCONT, data = dataCom)
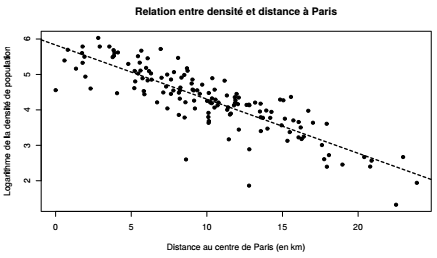
summary(lmDensDist)Le coefficient de détermination (R-squared) est égal à 0,72, ce qui indique que 72 % de la variation du logarithme de la densité de population des communes étudiées s'expliquent par la variation de leur distance au centre de Paris (en 2008). Le signe du paramètre kitxmlcodeinlinelatexdvpb_1finkitxmlcodeinlinelatexdvp confirme l'observation du sens de la relation sur le nuage de points : la distance au centre de Paris a un effet négatif sur la densité de population des communes de la petite couronne parisienne. Il indique que le logarithme de la densité varie en moyenne de 0,15 lorsque la distance au centre de Paris augmente d'un kilomètre. Le paramètre kitxmlcodeinlinelatexdvpb_0finkitxmlcodeinlinelatexdvp informe sur la valeur théorique de la densité de population lorsque la distance au centre de Paris est égale à 0.
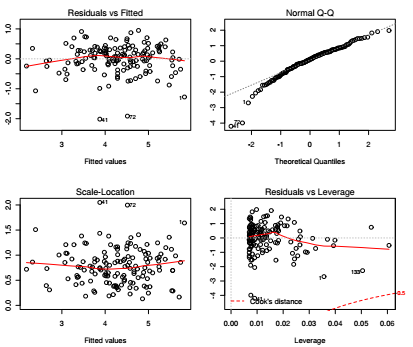
La fonction plot() appliquée aux résultats d'un modèle de régression linéaire obtenus par la fonction lm() permet de représenter les quatre principales hypothèses au cœur de ce modèle :
- la normalité des résidus par rapport aux valeurs prédites (en haut à gauche de l'image) ;
- la normalité globale des résidus (en haut à droite de l'image) ;
- la corrélation entre les valeurs de la variable explicative et le carré des résidus standardisés (en bas à gauche de l'image) ;
- l'existence de valeurs extrêmes altérant l'estimation des paramètres (en bas à droite de l'image).
Les figures renseignant sur la normalité des résidus (figures du haut) montrent que la variance des résidus a tendance à être constante, quelle que soit la valeur de la densité. Les estimations de la densité de population par la distance au centre sont aussi bonnes pour toute la gamme de valeurs de densité. En outre, la figure 3 (en bas à gauche) semble montrer qu'il n'y a pas d'autocorrélation des résidus puisque les valeurs de ces derniers ne sont pas déterminées par les valeurs de la variable dépendante. Les densités de population ne sont pas plus sur- ou sous-estimées par la distance au centre selon qu'elles sont faibles ou élevées.
Les objets spécifiques : les fonctions utilisées pour calculer des modèles statistiques renvoient des objets de type spécifique : objet lm pour la fonction lm() ou objet htest pour la fonction chisq.test() par exemple. Ces objets sont des listes qui stockent tous les éléments nécessaires au calcul et à l'interprétation du modèle. On accède à ces objets avec l'opérateur $ de la même façon qu'on accède à une colonne de data.frame : objetModele$residuals pour récupérer les résidus par exemple. Pensez à utiliser la touche Tab pour l'autocomplétion.
Pour améliorer le modèle, il serait intéressant de corriger la densité de population des 12e et 16e arrondissements, en effet presque la moitié de leur surface correspond aux bois de Boulogne et de Vincennes respectivement. Il serait aussi possible de recommencer l'analyse de régression sans intégrer les cas extrêmes (outliers). Le nuage de points est finalement affiché et la droite de régression est surimposée avec deux arguments graphiques : lty (line type) et lwd (line width).
|
Sélectionnez 1. 2. 3. 4. 5. 6. 7. 8. 9. |
|
|
L'analyse visuelle peut être complétée d'une cartographie des résidus du modèle : les outils de cartographie sont présentés dans le Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie.
V-C. Relation entre une variable quantitative et une variable qualitative▲
L'objectif de cet exercice est de décrire l'organisation spatiale de la richesse en Île-de-France : l'hypothèse est que le niveau départemental permet de résumer l'hétérogénéité de la richesse dans la région.
V-C-1. Représentation graphique de la relation▲
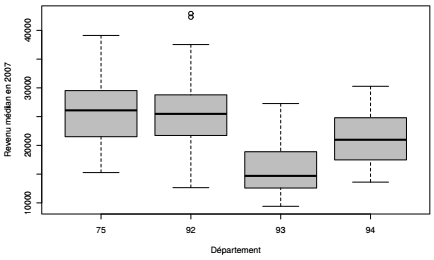
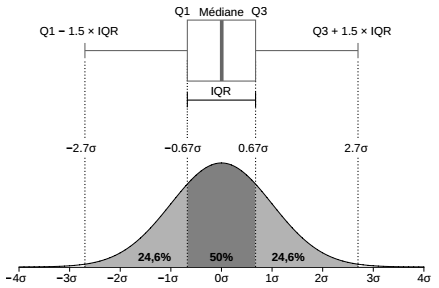
La fonction boxplot() est utilisée pour produire des graphiques appelés diagrammes en boîtes ou boîtes à moustaches (boxplot ou box-andwhisker plot). Ces graphiques résument visuellement la distribution statistique d'une variable quantitative autour de différentes mesures de centralité et de dispersion.
Dans le cas d'une analyse entre une variable quantitative et une variable qualitative, la boîte à moustaches montre la distribution de la variable quantitative pour chacune des modalités de la variable qualitative.
|
Sélectionnez 1. 2. 3. 4. 5. |
|
|
L'analyse visuelle donne une première idée des inégalités de revenus entre les quatre départements à l'étude : dans le 75 (Paris) et le 92 (Hauts-de-Seine), la médiane du revenu médian communal est d'environ 26 000 euros annuels, dans le 94 (Val-de-Marne) la médiane est de 21 000 euros et dans le 93 (Seine-Saint-Denis) elle est de moins de 15 000 euros. Un commentaire s'impose sur ce revenu « médian médian » : la variable RFUCQ207 est la médiane du revenu des individus calculé au niveau de la commune, en effet la mesure de centralité utilisée pour les variables de revenu est toujours la médiane parce que la distribution des revenus est très dissymétrique (le calcul du taux de pauvreté par exemple repose sur la médiane et non sur la moyenne). La boîte à moustaches indique la médiane au niveau départemental du revenu médian communal, cette mesure présente donc deux niveaux de résumé statistique et elle est différente du revenu médian des individus calculé au niveau départemental.
V-C-2. Analyse de la variance à un facteur▲
Une analyse de la variance à un facteur (ANOVA) est mise en place pour modéliser la relation entre le département d'appartenance des communes et le revenu médian communal. Il s'agit plus précisément de comparer les moyennes empiriques de la variable décrivant les revenus médians des communes pour les différents départements étudiés et la variabilité autour de ces moyennes. Deux options sont possibles avec R : (1) estimer les paramètres du modèle avec la fonction lm() puis analyser la variance avec la fonction anova(), ou (2) faire directement l'analyse de la variance avec la fonction aov(). Celle-ci présente la décomposition de la variance totale entre la variance due au facteur (variance intergroupe) et la variance résiduelle (ou variance intragroupe). Les deux solutions, qui offrent des résultats identiques, sont proposées ci-dessous.
Bien que la méthode employée transforme automatiquement la variable dépendante en variable catégorielle lors de la mise en place de l'ANOVA, il est préférable d'effectuer cette transformation en amont : (1) en vérifiant que la variable catégorielle est définie ou non comme telle dans le tableau avec la fonction is.factor(), et (2), dans le cas contraire, en la transformant à l'aide de la fonction as.factor().
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
# Transformation de la variable qualitative
is.factor(dataCom$CODDEP)
dataCom$CODDEP <- as.factor(dataCom$CODDEP)
# Anova - Option 1
lmRevDep <- lm(RFUCQ207 ~ CODDEP, data = dataCom)
anova(lmRevDep)
# Anova - Option 2
aovRevDep <- aov(RFUCQ207 ~ CODDEP, data = dataCom)
summary(aovRevDep)
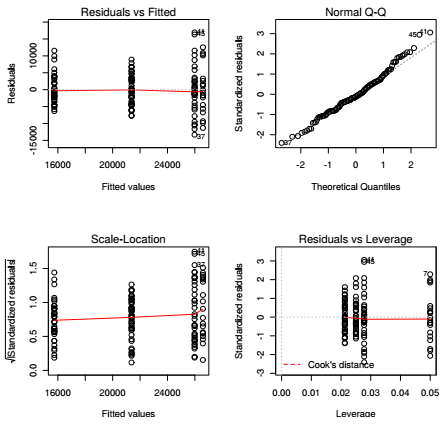
Les résultats du modèle sont donnés dans un tableau présentant les principaux éléments, à savoir la valeur F de Fisher, les degrés de liberté (df - degrees of freedom), la somme des carrés des écarts (Sum Sq), la moyenne des carrés des écarts (Mean Sq) et la p-value associée au test de Fisher (Pr > F). Tout comme avec le premier modèle de régression linéaire issu de la régression linéaire, on vérifie les conditions d'application du modèle ainsi construit, les plus importantes étant la normalité globale des résidus et leur homoscédasticité :
- la normalité des résidus par rapport aux valeurs prédites (en haut à gauche de l'image) ;
- la normalité globale des résidus (en haut à droite de l'image) ;
- la corrélation entre les valeurs de la variable explicative et le carré des résidus standardisés (en bas à gauche de l'image) ;
- l'existence de valeurs extrêmes altérant l'estimation des paramètres (en bas à droite de l'image).
Le graphique représentant les valeurs des résidus (residuals) contre les valeurs ajustées (fitted values) par départements, en haut à gauche, montre une variance plus grande pour les départements les plus riches (où la valeur estimée est la plus importante). Cela laisse suggérer une plus grande variabilité des situations observées et donc un moins bon ajustement du modèle aux communes de ces départements. Ces résultats sont répétés dans les deux graphiques du bas. Enfin, le quantile-quantile plot, en haut à droite de l'image, montre une droite relativement proche d'une droite à 45 degrés, avec de rares individus statistiques s'écartant de la droite hors des valeurs les plus élevées. Ceci indique une relative normalité de la distribution des résidus malgré une légère déviance pour les cas les plus extrêmes.
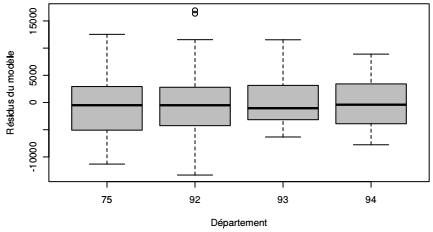
Les graphiques en boîtes à moustaches sont très utilisés pour l'exploration visuelle des résidus d'une analyse de la variance. Ceux-ci permettent également de mesurer le degré d'homoscédacité des résidus en offrant une lecture plus facile.
|
Sélectionnez 1. 2. 3. 4. 5. |
|
|
V-D. Relation entre deux variables qualitatives▲
L'objectif de cet exercice est d'analyser la relation entre le vote au référendum européen(16) et le département d'appartenance (CODDEP). L'hypothèse est que les départements les plus riches (75 et 92) ont massivement voté pour le « oui » et les départements les plus pauvres (93) pour le « non ».
V-D-1. Représentation graphique de la relation▲
Dans un premier temps, la variable de réponse au recensement est créée à partir de la variable REFEROUI qui donne le pourcentage de vote pour le « oui » au niveau des communes. Les communes affichant un vote supérieur à 50 % sont considérées comme globalement pour et celles affichant un vote inférieur à 50 % comme globalement contre.
2.
3.
dataCom$REPREF <- ifelse(dataCom$REFEROUI > 50,
"OUI",
"NON")
Le premier réflexe en présence de variables qualitatives est de faire des tableaux de dénombrement (selon une seule variable) et des tableaux de contingence (tris croisés selon deux variables), ce que permet de faire la fonction table().
2.
3.
4.
5.
6.
7.
8.
9.
crossTabDepRef <- table(dataCom$CODDEP, dataCom$REPREF)
crossTabDepRef
##
## NON OUI
## 75 0 20
## 92 6 30
## 93 36 4
## 94 24 23
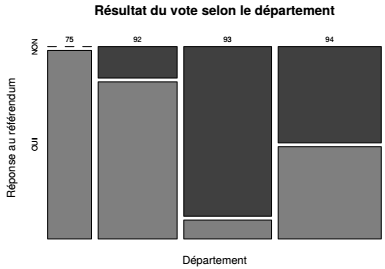
La fonction mosaicplot() complète cette première analyse. Il s'agit de la représentation graphique du tableau de contingence : la longueur des segments sur les deux axes correspond aux fréquences relatives correspondantes et l'aire des rectangles est également proportionnelle à la fréquence relative de la sous-population représentée. Par exemple, le département du Val-de-Marne (94) compte 43 communes, soit environ 33 % du total de 143 communes à l'étude : sur l'axe horizontal, la longueur du segment de ce département correspond donc au tiers de la longueur totale de l'axe. De même, 24 de ces 47 communes ont voté pour le « non » soit environ la moitié : sur l'axe vertical, la longueur du segment correspond donc à la moitié de la longueur totale de l'axe. Enfin, cette sous-population des communes du Val-de-Marne ayant voté pour le « non », composée de 24 communes, représente 17 % de l'ensemble à l'étude : la surface du rectangle correspondant fait également 17 % de la surface utile du graphique.
|
Sélectionnez 1. 2. 3. 4. 5. 6. |
|
|
V-D-2. Analyse de la répartition observée▲
Pour deux variables X et Y, comprenant respectivement m et n modalités, une sous-population est désignée par l'appartenance à une modalité de chacune des deux variables. Les communes du Val-de-Marne ayant majoritairement voté « non » au référendum sont un exemple de sous-population, leur effectif, au croisement des modalités des deux variables est dit « effectif conjoint ».
Le total marginal des lignes est noté kitxmlcodeinlinelatexdvpn_jfinkitxmlcodeinlinelatexdvp, celui des colonnes est noté kitxmlcodeinlinelatexdvpn_ifinkitxmlcodeinlinelatexdvp et l'effectif total est noté kitxmlcodeinlinelatexdvpn..finkitxmlcodeinlinelatexdvp.
Le tableau de contingence présenté plus haut contient des valeurs absolues, il peut utilement être transformé pour travailler sur des valeurs relatives. Trois types de proportions sont envisageables :
-
la proportion des effectifs conjoints sur l'effectif total ;
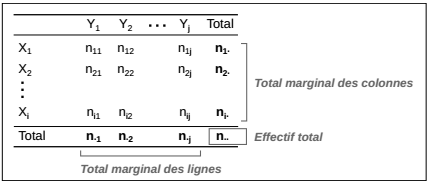
FIGURE 5.2 - Notation des effectifs dans un tableau de contingence -
la proportion des effectifs conjoints sur le total marginal des colonnes (profil ou pourcentage en ligne) ;
- la proportion des effectifs conjoints sur le total marginal des lignes (profil ou pourcentage en colonne).
Les profils en ligne et en colonne sont calculés ici en passant par la fonction prop.table(). Cette fonction demande comme argument un objet tabulé (le tableau de contingence) et non les variables qualitatives elles-mêmes. L'argument margin permet de spécifier le total de référence, celui des lignes (dimension 1), celui des colonnes (dimension 2) ou l'effectif total (option par défaut).
rowPct <- prop.table(crossTabDepRef, margin = 1)
colPct <- prop.table(crossTabDepRef, margin = 2)Les deux profils disent des choses bien différentes : le profil en ligne dit que 51,1 % des communes du Val-de-Marne (94) ont voté « non » au référendum, le profil en colonne dit que 36,3 % des communes qui ont voté « non » se trouvent dans le Val-de-Marne. Dans l'analyse de la relation entre les deux variables c'est le profil en ligne qui est intéressant parce que, par convention, un tableau de contingence présente la variable à expliquer (dépendante) en colonne et la variable explicative (indépendante) en ligne. Ici, la question est de savoir si l'appartenance départementale explique le vote au référendum, c'est donc la proportion qui rapporte le vote aux totaux départementaux qui est pertinente.
V-D-3. Analyse des écarts à l'indépendance▲
Le tableau de contingence dénombre les communes selon le croisement des modalités des deux variables, il donne la répartition observée. Cette répartition observée est comparée à une répartition théorique sous hypothèse d'indépendance, c'est-à-dire la répartition qu'on observerait s'il n'y avait aucun lien entre les deux variables. Cette répartition théorique consiste donc à redistribuer les effectifs conjoints tout en conservant les effectifs marginaux :
kitxmlcodelatexdvpn_{ij}^e = \frac{n_i n._j}{n..}finkitxmlcodelatexdvpLa fréquence conjointe espérée (kitxmlcodeinlinelatexdvpn_{ij}^efinkitxmlcodeinlinelatexdvp) est le produit des totaux marginaux en ligne (kitxmlcodeinlinelatexdvpn_i.finkitxmlcodeinlinelatexdvp) et en colonne (kitxmlcodeinlinelatexdvpn._jfinkitxmlcodeinlinelatexdvp) divisé par l'effectif total (kitxmlcodeinlinelatexdvpn..finkitxmlcodeinlinelatexdvp). L'analyse ci-dessous permet de déterminer l'existence d'un lien entre le département et le vote au référendum au niveau de la commune. L'observation du tableau de contingence laisse penser que la répartition de ce vote entre départements n'est pas homogène. Le test du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp calculé avec la fonction chisq.test() mesure la validité statistique d'une telle hypothèse.
L'objet créé par la fonction chisq.test() est de type htest, c'est une liste qui contient tous les éléments nécessaires à l'analyse : effectifs théoriques, résidus bruts ou résidus relatifs (cf. Encadré).
2.
3.
4.
5.
6.
7.
8.
9.
10.
chi2DepRef <- chisq.test(x = dataCom$CODDEP,
y = dataCom$REPREF)
chi2DepRef
##
## Pearson's Chi-squared test
##
## data: dataCom$CODDEP and dataCom$REPREF
## X-squared = 61.14, df = 3, p-value = 3.36e-13
Le test nous donne la statistique du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp (chi-squared), le degré de liberté associé au test (le produit du nombre de modalités - 1 de chacune des variables) et la significativité de la relation (valeur de p). La probabilité d'obtenir une valeur du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp observé aussi élevée dans un échantillon de la taille observée sous l'hypothèse d'indépendance des deux variables est inférieure à 0.001 %. Il est donc possible de rejeter l'hypothèse d'indépendance pour un risque de première espèce (rejeter l'hypothèse nulle alors que celle-ci est vraie, faux positif).
Il y a une relation entre les résultats du vote au référendum au niveau communal et le département d'appartenance des communes : dans les départements les plus riches (75 et 92), le résultat est massivement positif ; dans le département le plus pauvre (93), il est largement négatif ; dans le Val-de-Marne (94) les résultats sont équilibrés.
Au terme de ce chapitre, l'utilisateur connaît les principales fonctions permettant d'explorer et de modéliser des relations bivariées entre deux variables quantitatives, entre deux variables qualitatives ou entre une variable quantitative et une variable qualitative. Ces mêmes fonctions peuvent être utilisées pour modéliser des relations multivariées et faire, par exemple, des analyses de la variance à plusieurs facteurs ou des régressions linéaires multiples.