R et espace

Les algorithmes de classification visent à constituer des groupes différenciés d'individus homogènes au regard de leurs attributs statistiques. Les groupes sont homogènes si les individus statistiques qui les constituent sont les plus semblables possible au sein de chaque groupe, ils sont différenciés si les individus de groupes différents sont aussi dissemblables que possible.

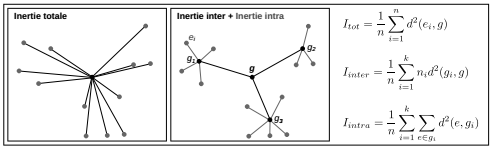
Le schéma suivant montre un exemple simple comprenant douze individus statistiques décrits par deux variables. L'inertie totale du nuage de points est la somme du carré des distances de chaque point au centre. Cette inertie totale peut être décomposée en une inertie intergroupe et une inertie intragroupe : la classification aura pour objectif de minimiser l'inertie intragroupe (homogénéité au sein du groupe) et de maximiser l'inertie intergroupe (différentiation entre groupes).

Les deux méthodes de classification les plus classiques sont le partitionnement direct de l'ensemble d'individus et la classification ascendante hiérarchique. La première méthode consiste à assigner un nombre de centres fixé a priori puis à localiser et relocaliser les centres ou affecter et réaffecter les individus à ces centres par un processus itératif qui optimise un critère de qualité de la partition. Ces algorithmes de « réallocation dynamique » (centres mobiles, nuées dynamiques) sont rapides et peuvent être appliqués sur des données massives.

La classification ascendante hiérarchique (CAH) est également un algorithme itératif. Il part d'une partition en n classes, chaque classe étant constituée d'un seul individu. À chaque étape, il agrège les deux classes les plus proches. Ce processus est répété n-1 fois, il produit ainsi une série hiérarchique de n-1 partitions, de la plus fine (n classes) à la plus grossière (une classe). Cette série de partitions est représentée par un arbre hiérarchique ou dendrogramme. À la différence des méthodes de partitionnement direct, la CAH permet à l'utilisateur de choisir le nombre de classes a posteriori, à partir de mesures et de graphiques d'aide à l'interprétation. Cette caractéristique explique l'usage fréquent de cette méthode en sciences sociales, cependant elle est beaucoup plus gourmande en calcul et ne peut être appliquée à de gros jeux de données.

Ce chapitre se concentre sur la méthode de classification ascendante hiérarchique parce qu'elle est très souvent utilisée en géographie. Les paramètres à définir sont la définition d'une distance entre individus et d'une distance entre classes. Ce type de distance entre classes est aussi appelé « critère d'agrégation ».

La distance kitxmlcodeinlinelatexdvpd(i,i')finkitxmlcodeinlinelatexdvp est la distance entre deux individus kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpi'finkitxmlcodeinlinelatexdvp. La classification s'appuie sur une matrice de distances entre individus que l'utilisateur doit définir : distance euclidienne, distance du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp ou autre. Dans les fonctions présentées par la suite, l'utilisateur peut fournir un tableau d'individus décrits par des variables quantitatives, il peut aussi fournir une matrice de distances calculée au préalable, par exemple avec la fonction dist(). Pour pouvoir raisonner en termes d'inertie inter et intraclasse, il faut travailler sur des distances euclidiennes au carré (cf. Figure 7.1).

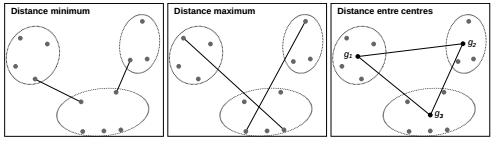
Le critère d'agrégation kitxmlcodeinlinelatexdvp\delta(k,k')finkitxmlcodeinlinelatexdvp définit la façon de mesurer la distance entre les classes kitxmlcodeinlinelatexdvpkfinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpk'finkitxmlcodeinlinelatexdvp. Plusieurs critères peuvent être utilisés :

• distance minimum ;
• distance maximum ;
• distance moyenne ;
• distance entre centres de gravité ;
• moyenne des distances à l'intérieur des classes ;
• perte d'inertie minimum (critère de Ward), fondée sur la décomposition de l'inertie totale en inertie intra- et interclasses.

La Figure 7.2 montre trois de ces critères d'agrégation. Cet exemple simple ne comporte que deux variables pour permettre de bien visualiser le travail sur les distances. Au-delà de trois dimensions, les distances ne sont plus visualisables, mais elles restent calculables et le principe d'agrégation reste le même.

Chacun des critères d'agrégation a ses inconvénients, certains ont tendance à créer des classes de tailles très hétérogènes, d'autres ont tendance à systématiquement créer des groupes de même taille, certains sont très sensibles aux valeurs extrêmes. Dans tous les cas, l'utilisateur doit prendre toutes les précautions nécessaires pour arriver à un résultat cohérent : faire des tests en faisant varier les paramètres, bien utiliser les aides à l'interprétation pour choisir le nombre de classes, examiner la classification obtenue.

Pour déterminer le nombre de classes optimal, l'arbre hiérarchique, ou dendrogramme, est un outil visuel efficace. Les feuilles de l'arbre sont les n classes formées chacune d'un seul individu avant la première étape d'agrégation. À chaque étape, elles sont regroupées selon le critère d'agrégation choisi et la position sur l'axe vertical du nœud formé à chaque regroupement donne une mesure de la dissimilarité entre classes.

Pour la lecture des partitions, on peut imaginer que l'on parcourt l'arbre du bas vers le haut avec une règle horizontale. La règle coupe l'arbre en 2. La partie inférieure donne les classes associées (ensemble des nœuds directement inférieurs). L'axe vertical marque les valeurs du critère d'agrégation (mesure de dissimilarité) à chaque étape de l'algorithme. Ainsi, la compacité des classes créées se lit sur cet axe en examinant la longueur des branches associées aux nœuds inférieurs.

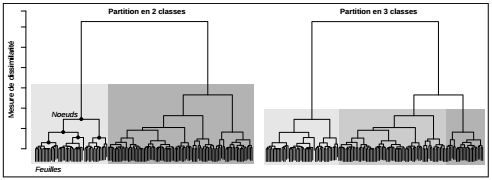
Au-delà de la lecture de l'arbre, il existe un grand nombre de graphiques d'aide à l'interprétation et d'indicateurs du nombre optimal de classes à adopter. Dans tous les cas, il ne faut jamais considérer qu'il existe une unique partition possible. Pour construire une classification robuste et en comprendre le résultat, il faut systématiquement examiner les classes, leur effectif, leur compacité (distance entre les individus regroupés), leur séparation des autres classes. Il est aussi utile d'examiner les individus exceptionnels, ceux qui sont très proches du centre de classe et ceux qui en sont très éloignés. Il convient enfin d'examiner au sein de chaque classe la distribution des variables utilisées pour la classification.

Pour s'assurer de la robustesse d'une classification, il existe des méthodes plus avancées : les méthodes mixtes, qui combinent la classification hiérarchique avec le partitionnement direct(18) ; le couplage de la classification avec l'analyse factorielle. Ce procédé est utile dans le cas où les variables utilisées pour la classification sont corrélées les unes avec les autres.

La suite du chapitre présente deux applications : la classification d'individus décrits par des variables quantitatives et la classification de lignes d'un tableau de contingence. La première utilisera la distance euclidienne passée au carré, la seconde est couplée à une analyse factorielle des correspondances et travaille sur une matrice de distances du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp.

Il s'agit dans cette section de classer les communes en fonction de leur composition en catégories professionnelles (CSP). Cette classification est faite sur les variables qui renseignent les proportions de ces catégories en 2007 : proportions d'artisans, de cadres, de professions intermédiaires, d'employés et d'ouvriers. Les ordres de grandeur de ces variables étant différents, elles doivent être centrées-réduites de manière à donner à chacune le même poids dans l'analyse.

selecVar <- c("PART07", "PCAD07", "PINT07", "PEMP07", "POUV07")
muniCSP <- socEco9907[, selecVar]
muniCSP <- scale(muniCSP)

La classification se fait avec la fonction agnes() (agglomerative nesting) du package cluster. La fonction permet de spécifier la distance entre individus, ici la distance euclidienne, et la distance entre classes, ici le critère de Ward précédemment décrit.

cahCSP <- agnes(muniCSP,
                metric = "euclidean",
                method = "ward")

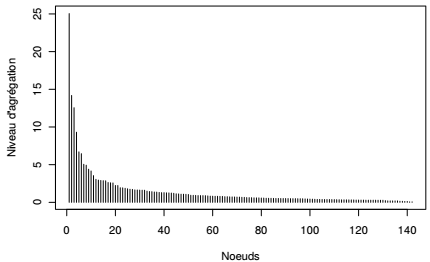
L'objet cahCSP est de type agnes. Il contient l'ensemble des informations qui vont ensuite servir pour dessiner et analyser l'arbre, puis le couper et donner des aides à l'interprétation. Le plus simple de ces graphiques est le diagramme de niveaux : il représente la valeur de la mesure de dissimilarité associée à la création de chacun des nœuds. Cette valeur dépend du critère d'agrégation choisi, dans le cas présent, il s'agit de la part de l'inertie interclasse qui, à chaque étape d'agrégation, passe en inertie intraclasse. Au début du processus, chaque classe est composée d'un seul individu, l'inertie totale est donc égale à l'inertie interclasse. À la fin du processus, il n'y a plus qu'une seule classe, l'inertie totale est donc égale à l'inertie intraclasse.

On accède aux niveaux par l'attribut $height de l'objet. Ceux-ci peuvent être triés par ordre décroissant puisque, par définition, l'algorithme agrège à chaque étape les classes les moins dissemblables.

sortedHeight <- sort(cahCSP$height, decreasing = TRUE)
plot(sortedHeight,
     type = "h",
     xlab = "Noeuds",
     ylab = "Niveau d'agrégation")

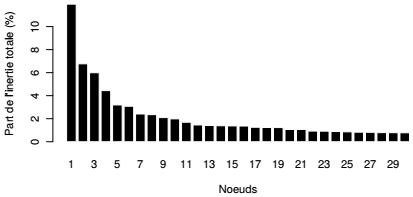
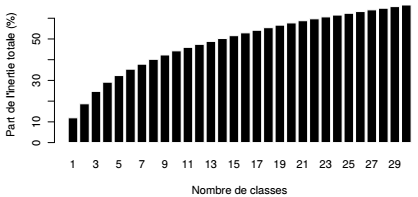
Un tel graphique permet d'ores et déjà de repérer les « sauts » et de décider à quel niveau on peut couper l'arbre. Les niveaux sont exprimés ici en absolu et, lorsque l'on utilise le critère d'agrégation de Ward, il est d'usage de les exprimer en proportion de l'inertie totale : chaque niveau est donc rapporté à la somme des niveaux. En cumulant ce taux de proche en proche, on obtient la part de l'inertie restituée par la partition correspondante. Représenter le haut de la hiérarchie est suffisant, ici les 30 derniers nœuds.

Attention, pour une telle interprétation, la distance entre classes utilisée par le critère d'agrégation de Ward doit être une distance euclidienne passée au carré. Comme mentionné précédemment, la fonction agnes() accepte deux types d'objets : un tableau d'individus caractérisés par des variables ou une matrice de distances calculée au préalable. Si l'utilisateur décide de calculer la matrice de distances, avec la fonction dist() par exemple, il faut qu'il la passe au carré avant de faire la classification. En revanche, si l'utilisateur donne comme argument un tableau individus-variables et paramètre la fonction comme fait plus haut (distance euclidienne et critère de Ward), la fonction travaille automatiquement sur des distances euclidiennes au carré.

relHeight <- sortedHeight / sum(sortedHeight) * 100
cumHeight <- cumsum(relHeight)

barplot(relHeight[ 1: 30], names.arg = seq(1, 30, 1),
        col = "black", border = "white", xlab = "Noeuds",
        ylab = "Part de l'inertie totale (%)")

barplot(cumHeight[ 1: 30], names.arg = seq(1, 30, 1),
        col = "black", border = "white",
        xlab = "Nombre de classes",
        ylab = "Part de l'inertie totale (%)")

On lit ainsi à la fois les sauts (graphique du haut) et la part de l'inertie interclasse par rapport à l'inertie totale associée à la partition (graphique du bas). Une coupure en 2, en 4 ou en 5 classes semble judicieuse.

VII-B-1. Coupure de l'arbre et description des classes▲

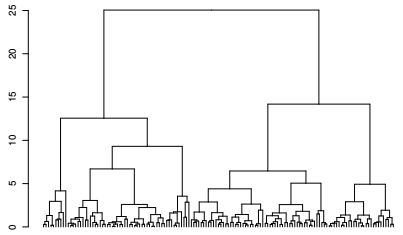
Il y a plusieurs façons d'afficher l'arbre hiérarchique, la première consiste à utiliser la fonction pltree() du package cluster directement sur l'objet créé par la classification. Pour plus de réglages graphiques, il est utile de transformer au préalable cet objet de type agnes en objet de type dendrogram puis d'appliquer à cet objet la fonction générique plot().

Sélectionnez 1. 2. dendroCSP <- as.dendrogram(cahCSP) plot(dendroCSP, leaflab = "none")

La visualisation de l'arbre confirme les remarques précédentes, une partition en quatre classes semble pertinente. Pour appuyer cette décision, un grand nombre d'indicateurs existent dont les principaux sont regroupés dans le package NbClust. Celui-ci contient une seule fonction qui calcule trente indicateurs de ce type et donne le nombre de partitions optimal selon chacun d'eux.

Pour découper l'arbre et obtenir la partition voulue, c'est la fonction cutree() qui est utilisée. Celle-ci crée une nouvelle variable donnant pour chaque entité son numéro de classe. Cette variable peut ensuite être intégrée au tableau initial pour caractériser les classes au regard des variables utilisées pour la classification.

 

Sélectionnez

1.
2.
3.
4.
5.

clusCSP <- cutree(cahCSP, k = 4)
muniCSP <- as.data.frame(muniCSP)
muniCSP$CLUSCSP <- factor(clusCSP,
                          levels = 1: 4,
                          labels = paste("CLUS", 1: 4))

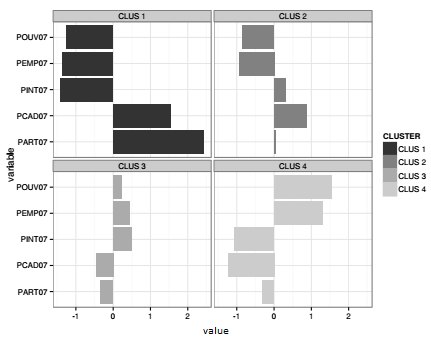
L'analyse la plus simple consiste à visualiser la moyenne de classe de chacune des variables. Ce travail peut être mené sur les variables originelles, les proportions de chacune des catégories socioprofessionnelles, mais aussi sur les variables centrées-réduites. La première option a l'avantage de l'unité de mesure (%) qui est directement interprétable. La seconde option permet une comparaison directe des profils à partir de variables aux ordres de grandeur très différents. C'est cette seconde option qui est choisie ici.

Dans un premier temps, la moyenne des variables est calculée avec la fonction aggregate() sur chacun des quatre groupes créés par la classification. On cherche ensuite à faire un diagramme en bâtons (barplot) pour représenter graphiquement chacun des groupes. Ceci pourrait être fait avec une boucle qui afficherait successivement les graphiques. Il faudrait également modifier les paramètres graphiques pour que chaque graphique s'intègre dans la même sortie. Dans l'exemple suivant, cette représentation est produite avec le package ggplot2 présenté dans le Chapitre 9CHAPITRE 9 Focus sur la visualisation graphique. Ce package demande un tableau en format long (cf. Section 2.4.3Transposition variables-observations), transformation effectuée avec la fonction melt().

 

Sélectionnez

1.
2.
3.
4.
5.
6.

clusProfile <- aggregate(muniCSP[, 1: 5],
                         by = list(muniCSP$CLUSCSP),
                         mean)

colnames(clusProfile)[ 1] <- "CLUSTER"
clusLong <- melt(clusProfile, id.vars = "CLUSTER")

Le graphique prend comme argument le tableau qui vient d'être transformé, les trois variables sont l'identification des classes (CLUSTER), l'identification des variables (variable) et les valeurs prises par les variables pour chaque classe (value). Pour construire une planche de graphiques, il faut inclure dans une même sortie graphique un ensemble de graphiques correspondant à des sous-groupes. C'est la fonction facet_wrap() qui permet cette mise en forme (cf. Section 9.3.4Construction d'une planche).

Sélectionnez 1. 2. 3. 4. 5. 6. ggplot(clusLong) + geom_bar(aes(x = variable, y = value, fill = CLUSTER), stat = "identity") + scale_fill_grey() + facet_wrap(~ CLUSTER) + coord_flip() + theme_bw()

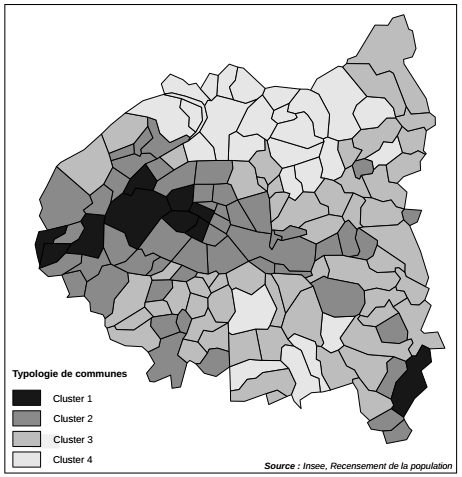
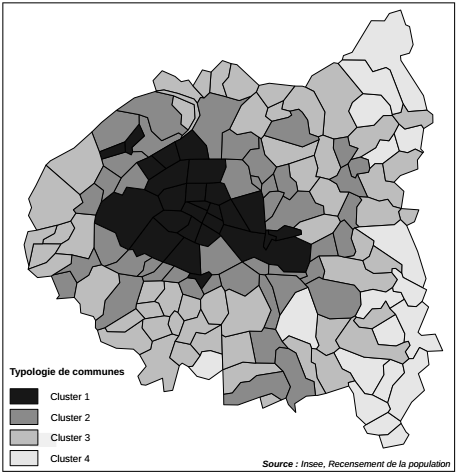
Ces profils peuvent être cartographiés(19) avec les méthodes présentées dans les chapitres 9 et 10. L'analyse conjointe de la carte et du graphique montre un Ouest parisien accompagné de quelques communes des Hauts-de-Seine (cluster 1) avec une forte surreprésentation des cadres et des artisans-commerçants. À l'opposé, le Nord de la zone d'étude, correspondant à la moitié Est de la Seine-Saint-Denis (cluster 4), montre une forte surreprésentation d'ouvriers et d'employés. Entre ces deux extrêmes, les profils 2 et 3 sont comparables aux profils 1 et 4 respectivement, mais avec des tendances moins marquées.

Certains cas particuliers pourraient être examinés par une analyse plus fine des profils de classes les comparant au profil moyen de l'ensemble de l'espace d'étude. Il s'agirait de tester, pour chaque variable, si la moyenne de la classe est significativement différente de la moyenne générale. Tous ces calculs pourraient être faits avec les fonctions présentées dans les chapitres 4 et 5. Il existe aussi une fonction tout-en-un, la fonction catdes() du package FactoMineR.

Cet exemple simple de classification montre aussi l'intérêt de coupler les méthodes, en particulier l'analyse factorielle et la classification. Il arrive en effet souvent que les variables d'intérêt soient corrélées les unes avec les autres, cas systématique lorsque les variables sont des pourcentages qui somment 100 % pour chaque individu statistique. Ici, les communes avec une forte proportion de cadres et d'artisans-commerçants auront mécaniquement une faible proportion des autres catégories. Dans un tel cas, il est judicieux d'effectuer d'abord une analyse factorielle sur les variables d'intérêt, analyse qui élimine les problèmes de colinéarité, puis de faire une classification sur les axes factoriels.

VII-C-1. Classification sur une métrique du χ2▲

popEvol <- popCom3608[ , 3: 11]
row.names(popEvol) <- popCom3608$CODGEO
coaPop <- dudi.coa(popEvol,
                   scannf = FALSE,
                   nf = ncol(popEvol))

library(FactoClass)
chiDist <- dist.dudi(coaPop, amongrow = TRUE)
cahPop <- ward.cluster(chiDist,
                       peso = apply(popEvol, 1, sum),
                       plots = FALSE, h.clust = 1)
popEvol$CLUSTER <- paste("CLUS", cutree(cahPop, k = 4))

VII-C-2. Description des classes▲

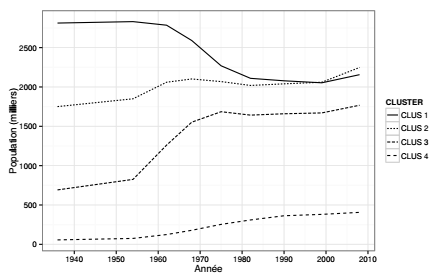
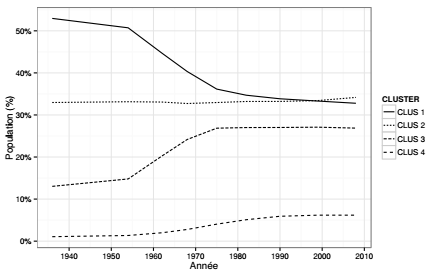
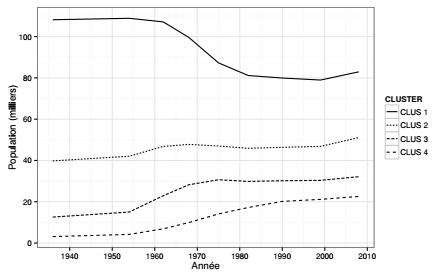
Le tableau de contingence représente ici les trajectoires des communes en termes de peuplement. La description des classes proposée dans cette section se concentre sur l'analyse des groupes de communes pour lesquelles les trajectoires de peuplement sont semblables. Trois types de tableaux sont créés à partir de résumés numériques calculés sur les classes de communes : un tableau qui donne la somme des populations communales des classes à chaque pas de temps, un tableau qui rapporte cette somme à la population totale de l'espace d'étude, un tableau qui donne la population communale moyenne pour chaque classe et à chaque pas de temps.

La fonction aggregate() est d'abord utilisée pour calculer les résumés numériques selon la variable de regroupement CLUSTER (cf. Section 2.4.2Agrégations et traitements par blocs). Les effectifs sont divisés par 1000 pour une meilleure lisibilité (population exprimée en milliers). Le calcul des populations en pourcentage du total à chaque date est fait avec la fonction prop.table()présentée précédemment (cf. Section 5.4.2Analyse de la répartition observée). Cette fonction demande une transformation du tableau en objet de type matrix, puis une transformation du résultat en objet de type data.frame. Le calcul des populations moyennes se fait comme le premier avec aggregate() mais en utilisant la fonction mean() au lieu de sum().

 

Sélectionnez

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.

# Somme des populations (absolue)
sumClass <- aggregate(popEvol[ , 1: 9],
                      by = list(popEvol$CLUSTER),
                      FUN = sum)
sumClass[ , 2: 10] <- sumClass[ , 2: 10] / 1000
colnames(sumClass)[ 1] <- "CLUSTER"

# Somme des populations (relative)
sumClassMat <- as.matrix(sumClass[ , 2: 10])
propClass <- as.data.frame(prop.table(sumClassMat, 2))
propClass$CLUSTER <- sumClass$CLUSTER

# Moyenne des populations
meanClass <- aggregate(popEvol[ , 1: 9],
                       by = list(popEvol$CLUSTER),
                       FUN = mean)
meanClass[ , 2: 10] <- meanClass[ , 2: 10] / 1000
colnames(meanClass)[ 1] <- "CLUSTER"

Comme dans la section précédente, il est possible de produire des représentations graphiques avec les fonctions génériques ou avec le package ggplot2. C'est cette option qui est choisie et les tableaux doivent donc être transformés en format long avec la fonction melt(). Ensuite, une variable temporelle est créée à partir des noms de variables (POP1936, POP1954, etc.) : les quatre derniers caractères sont extraits avec la fonction substr() et ils sont transformés en nombres entiers.

 

Sélectionnez

1.
2.
3.
4.
5.
6.

absSum <- melt(sumClass, id.vars = "CLUSTER")
relSum <- melt(propClass, id.vars = "CLUSTER")
popMean <- melt(meanClass, id.vars = "CLUSTER")
absSum$YEAR <- as.integer(substr(absSum$variable, 4, 7))
relSum$YEAR <- as.integer(substr(relSum$variable, 4, 7))
popMean$YEAR <- as.integer(substr(popMean$variable, 4, 7))

Ces tableaux servent à produire les trois graphiques : somme des populations (valeur absolue), somme des populations (valeur relative) et moyenne des populations par classes.

Sélectionnez 1. 2. 3. 4. 5. 6. 7. ggplot(absSum) + geom_line(aes(x = YEAR, y = value, linetype = CLUSTER)) + scale_x_continuous("Année", breaks = seq(1930, 2010, 10)) + scale_y_continuous("Population (milliers)", breaks = seq(0, 2500, 500)) + theme_bw()

Sélectionnez 1. 2. 3. 4. 5. 6. 7. ggplot(relSum) + geom_line(aes(x = YEAR, y = value, linetype = CLUSTER)) + scale_x_continuous("Année", breaks = seq(1930, 2010, 10)) + scale_y_continuous("Population (%)", labels = percent) + theme_bw()

Sélectionnez 1. 2. 3. 4. 5. 6. 7. ggplot(popMean) + geom_line(aes(x = YEAR, y = value, linetype = CLUSTER)) + scale_x_continuous("Année", breaks = seq(1930, 2010, 10)) + scale_y_continuous("Population (milliers)", breaks = seq(0, 100, 20)) + theme_bw()

Ces graphiques renvoient une image assez claire des dynamiques de peuplement en distinguant ces quatre classes de communes : la première classe se caractérise par une forte diminution, particulièrement marquée entre les années 1960 et 1980, les trois autres se caractérisent par une augmentation continue, assez faible pour la classe 2, et forte pour les classes 3 et 4. Une représentation cartographique des classes de communes(21) est utile pour spatialiser ce constat : les quatre classes s'organisent, à peu de choses près, en cercles concentriques autour de Paris.

Ce chapitre a présenté plusieurs techniques de classification permettant de créer des groupes différenciés d'individus homogènes. La classification ascendante hiérarchique est une technique fréquemment utilisée en analyse spatiale, elle peut être mobilisée dans une approche descriptive, exploratoire et/ou modélisatrice.