R et espace

Le fichier MobResid08.txt est utilisé ici, il s'agit du fichier de mobilités résidentielles entre communes de la petite couronne produit par l'Insee.

mobResid <- read.csv2("data/MobResid08.txt",
                      stringsAsFactors = FALSE)

Le fichier de départ liste les flux résidentiels entre les communes de Paris et petite couronne entre 2003 et 2008. Il comprend 5 colonnes et 15 178 lignes, ses variables sont décrites à la Section 1.6L'exemple et les données. Il faut d'ores et déjà noter que le tableau est en format long : une ligne du tableau est un couple de lieux assorti d'un flux. Avec les techniques présentées à la Section 2.4.3Transposition variables-observations, il serait facile de passer à un format large, qui serait ici une matrice origine-destination.

Dans le langage de l'analyse de graphe, le format long est considéré comme une liste de liens (edges list) et le format large comme une matrice d'adjacence (adjacency matrix). L'exemple ci-dessous montre trois représentations d'un même graphe : une liste de liens, une matrice d'adjacence et une visualisation du graphe correspondant. Ce graphe de trois nœuds a les mêmes caractéristiques que le graphe des communes de l'agglomération parisienne sur lequel porte ce chapitre : c'est un graphe orienté et valué. Il est orienté parce qu'un flux de kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp vers kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp n'est pas équivalent à un flux de j vers i, ce qui se traduit par une matrice d'adjacence non symétrique. Il est valué parce que les liens sont assortis d'un attribut numérique qui associe une quantité au lien, par exemple le nombre d'individus qui migrent d'une commune vers une autre.

Les packages utilisés ici permettent de créer un graphe à partir des deux types de tableaux : liste de liens ou matrice d'adjacence. Cependant, avant de faire cette transformation du tableau en graphe, il convient de remarquer que bon nombre de mesures pourraient être calculées directement sur les tableaux, sans passer par la transformation en graphe. L'exemple ci-dessous montre un tel traitement qui vise à calculer un solde résidentiel relatif, mesure qui met en relation les flux entrant et sortant d'une commune.

Dans un premier temps, les flux intracommunaux sont supprimés pour simplifier le traitement et son interprétation(23). Seuls trois champs sont conservés et réordonnés : la commune d'origine (DCRAN), la commune de destination (CODGEO) et le flux (NBFLUX).

Dans un deuxième temps, le tableau long (liste de liens) est transformé en tableau large (matrice d'adjacence) avec le package reshape2 (cf. Section 2.4.3Transposition variables-observations). Ce tableau est un objet de type data.frame, il est transformé en objet de type matrix et les codes des communes d'origine sont ajoutés en tant que noms de lignes (avec row.names()) et non en tant que variable du tableau. Enfin, les flux entrants (in) et sortants (out) sont calculés grâce à la fonction apply() (cf. Section 3.4L'application de fonctions sur des ensembles).

library(reshape2)
edgesList <- mobResid[mobResid$CODGEO != mobResid$DCRAN,
                      c("DCRAN", "CODGEO", "NBFLUX")]

adjMat <- dcast(data = edgesList,
                formula = DCRAN ~ CODGEO,
                value.var = "NBFLUX")

adjMat <- as.matrix(adjMat[ , -1])
row.names(adjMat) <- colnames(adjMat)

flowsOut <- apply(adjMat, 1, sum, na.rm = TRUE)
flowsIn <- apply(adjMat, 2, sum, na.rm = TRUE)
summary(flowsOut)

##    Min. 1st Qu. Median Mean 3rd Qu.  Max.
##     168    2370   3850 5940    7010 34200

Une fois les flux entrants et sortants calculés, ils sont regroupés dans un nouveau tableau. Dans le vocabulaire de l'analyse de graphes, ce qui vient d'être calculé est le degré des nœuds pondéré par le flux (ce même calcul sera fait sur le graphe à la Section 8.3Mesures locales et manipulation du graphe). Ici la commune qui présente le flux sortant maximum envoie 34 200 individus vers les autres communes de l'espace d'étude. Enfin, les soldes résidentiels sont calculés : solde absolu d'abord, qui est la différence entre les flux entrants et les flux sortants ; solde relatif ensuite, qui est un rapport entre le solde absolu et la somme des flux.

flowsSum <- data.frame(CODGEO = names(flowsIn),
                       FLOWSOUT = flowsOut,
                       FLOWSIN = flowsIn,
                       stringsAsFactors = FALSE)

flowsSum$ABSDELTA <- flowsSum$FLOWSOUT - flowsSum$FLOWSIN
flowsSum$RELDELTA <- with(flowsSum, ABSDELTA /
                           (FLOWSOUT + flowsSum$FLOWSIN))

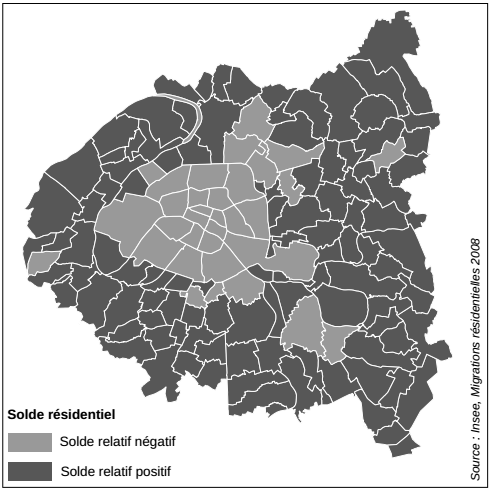
Ces variables qui mesurent les soldes résidentiels absolu et relatif peuvent être cartographiées avec les techniques présentées dans le Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie. Voici le résultat obtenu(24) : sans surprise, les soldes négatifs correspondent aux arrondissements parisiens et à quelques communes limitrophes, les soldes positifs correspondent au reste des communes de la petite couronne. Ce résultat ne concerne que le système de flux entre Paris et la petite couronne, pour une analyse plus complète il faudrait élargir l'analyse à l'ensemble de la région Île-de-France, de la France et/ou du monde.

VIII-B-1. Importation et exportation de graphes▲

Dans l'exemple ci-dessous, un graphe est créé à partir d'un tableau de flux entre des communes. La manipulation du tableau et sa transformation en graphe sont intégrées dans un flux de travail entièrement effectué avec le logiciel R. Cependant, il arrive que l'utilisateur récupère des données sous un format spécifique, propre aux logiciels d'analyse de graphes, ou bien qu'il veuille exporter un graphe créé avec R vers un autre logiciel de ce type, Ucinet ou Gephi par exemple.

Les deux packages présentés ici, statnet et igraph, disposent de fonctions pour importer (read) et exporter (write) les graphes dans des formats de données spécifiques. Avec statnet, ces fonctions prennent le nom du format à importer, par exemple read.paj() pour un format Pajek. Avec igraph, les fonctions sont read.graph() et write.graph() et le format est précisé dans les arguments des fonctions (pajek, gml, graphml, etc.).

En termes de calculs, R n'a rien à envier aux logiciels spécialisés tels que Ucinet ou Gephi. La principale raison pour laquelle un utilisateur pourrait vouloir utiliser l'un de ces logiciels réside dans la visualisation statique et/ou interactive du graphe.

VIII-B-2. Création d'un graphe avec R▲

library(statnet)
edgesMat <- as.matrix(edgesList[ , 1: 2])
residNet <- network(edgesMat, directed = TRUE)
set.edge.attribute(residNet,
                   attrname = "NBFLUX",
                   value = edgesList$NBFLUX)

library(igraph)
residGraph <- graph.data.frame(edgesList, directed = TRUE)

VIII-B-3. Calcul de mesures globales▲

residGraph
graph.density(residGraph)
clusters(residGraph)
diameter(residGraph)

Les mesures locales sont les mesures qui renseignent sur chaque sommet ou chaque lien du graphe, les plus courantes sont les suivantes :

• le degré : nombre de liens incidents pour un sommet. Dans un graphe orienté, on distingue le degré entrant et le degré sortant ;
• le degré pondéré : nombre de liens incidents pondéré par le poids de ces liens ;
• la famille de mesures (centralité, accessibilité) qui s'appuient sur le calcul des plus courts chemins.

Les mesures qui s'appuient sur le calcul des plus courts chemins peuvent être calculées aussi bien pour les nœuds que pour les liens. L'utilisateur peut souvent choisir de calculer ces mesures sur le graphe en prenant en compte une pondération des liens, c'est-à-dire un attribut quantitatif attaché aux liens. Les fonctions permettant de calculer ces différents indicateurs sont listées dans le tableau suivant.

Le calcul des degrés pondérés et non pondérés rejoint le calcul fait dans la première section de ce chapitre. Le degré pondéré donne une idée de la masse qui est envoyée ou reçue alors que le degré non pondéré donne une idée de la variété des destinations ou des origines. La commune qui a le flux sortant maximum envoie 34 200 individus vers les autres communes de l'espace d'étude, la commune qui a la plus grande variété de destinations envoie des individus vers 138 autres communes distinctes, c'est-à-dire vers la presque totalité de cet espace.

degOut <- degree(residGraph, mode = "out")

wtdDegOut <- graph.strength(residGraph,
                            mode = "out",
                            weights = E(residGraph) $NBFLUX)
summary(degOut)

##   Min. 1st Qu. Median  Mean 3rd Qu.  Max.
##   23.0    93.5  111.0 104.0   124.0 138.0

summary(wtdDegOut)
##   Min. 1st Qu. Median Mean 3rd Qu.  Max.
##    168    2370   3850 5940    7010 34200

Pour manipuler les attributs du graphe, la syntaxe est différente selon le package utilisé, statnet ou igraph. Avec igraph, il est possible de lire et d'écrire des attributs de nœuds et des liens avec les fonctions V() (V pour vertices) et E() (E pour edges), suivies de l'opérateur $ , suivi du nom de l'attribut. C'est cette syntaxe qui vient d'être utilisée pour pondérer les liens par la variable de flux : E(residGraph)$NBFLUX.

Ces fonctions peuvent être utilisées pour faire appel à un attribut du graphe (lire l'attribut), mais aussi pour enrichir le graphe de nouveaux attributs (écrire l'attribut dans l'objet). Dans cet exemple, un attribut est ajouté aux nœuds, le degré sortant. En exécutant l'objet ou avec la fonction summary(), on vérifie que l'ajout a été fait : il y a bien un nouvel attribut nommé DEGOUT, qui caractérise les nœuds (v) et qui est numérique (n).

V(residGraph) $DEGOUT <- degree(residGraph, mode = "out")
residGraph

## IGRAPH DN-- 143 14935 --
## + attr: name (v/c), DEGOUT (v/n), NBFLUX (e/n)

Si l'utilisateur enrichit le graphe sur lequel il travaille avec de nouveaux attributs et qu'il veut récupérer l'ensemble pour le traiter sous forme de tableau, la fonction get.data.frame() permet cette transformation.

C'est une pratique fréquente de chercher à l'intérieur d'un graphe des sous-groupes cohérents, c'est-à-dire des sous-graphes fortement connexes : des cliques (sociologues), des communautés (physiciens) ou des clusters (informaticiens). De nombreuses méthodes existent pour détecter ces sous-graphes et seules les principales sont évoquées.

Une première famille de méthodes s'appuie sur la notion de clique, terme qui désigne un sous-graphe maximal complet comprenant au moins trois sommets. En d'autres termes, une clique est un ensemble de sommets (au moins 3), entre lesquels tous les liens possibles sont présents (graphe complet) et il n'est pas possible d'ajouter un sommet sans que la propriété précédente ne disparaisse (graphe maximal). Cette définition est rarement opérationnelle, elle peut être trop restrictive (cas d'un réseau de connaissances dont les liens sont ténus) ou pas assez restrictive. C'est le cas ici sur le graphe des mobilités résidentielles dont la densité est très forte. Plusieurs paramètres permettent de moduler la définition de la clique pour l'assouplir ou au contraire la restreindre.

Il y a principalement deux façons d'assouplir la définition de la clique : jouer sur la distance et jouer sur les degrés. Au lieu de considérer un ensemble de sommets entre lesquels tous les liens possibles sont présents (distance de 1), il est possible de considérer une distance plus grande : par exemple, chaque sommet doit être relié à tous les autres avec une distance de 2. Ceci revient, dans un réseau social, à considérer que deux individus non reliés directement, mais qui connaissent un même individu tiers sont effectivement reliés à une distance 2 (l'ami d'un ami est mon ami). Le type de cliques formées de cette façon est appelé n-cliques.

En assouplissant le critère du degré, on peut créer des sous-ensembles dans lesquels tous les sommets sont connectés à k sommets de la clique (kcore) ou encore des sous-ensembles dans lesquels tous les liens possibles moins k sont présents (k-plex).

Les fonctions disponibles pour calculer ces sous-ensembles sont : clique.census() et kcores() pour le package statnet ; cliques() et graph.coreness() pour le package igraph. Avec statnet, la fonction clique.census() permet d'obtenir la taille des différentes cliques présentes, leur composition, le nombre de cliques auxquelles appartient chaque sommet et enfin les coappartenances de sommets entre les différentes cliques. Avec igraph, il y a des fonctions qui renvoient uniquement le nombre de cliques, cliques.number() par exemple, et des fonctions qui renvoient l'appartenance des sommets aux cliques, cliques() par exemple.

Ces approches sont plus adaptées pour des réseaux sociaux que pour le cas étudié ici. En effet, le graphe utilisé est très dense et le poids des liens (i.e. le flux résidentiel) porte une information très importante qui doit nécessairement être prise en compte dans le calcul de sous-ensembles. Il existe un grand nombre de méthodes pour créer des sous-ensembles cohérents qui s'appuient sur la modularité. Ces méthodes sont plutôt utilisées par les physiciens, on les retrouvera donc dans le package igraph plutôt que dans le package statnet.

Pour un graphe dans lequel on distingue plusieurs communautés, la modularité est forte quand les liens intracommunautés sont forts et les liens intercommunautés sont faibles. Cette mesure s'applique à des graphes non orientés, mais elle peut prendre en compte le poids des liens. Elle est définie comme la différence entre la proportion observée de liens intracommunauté et la proportion que l'on observerait dans un graphe aléatoire conservant la distribution de degrés du graphe originel :

Où kitxmlcodeinlinelatexdvpmfinkitxmlcodeinlinelatexdvp est la somme de la matrice de poids, où kitxmlcodeinlinelatexdvpA_{ij}finkitxmlcodeinlinelatexdvp est le poids du lien

entre kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp et où la fonction kitxmlcodeinlinelatexdvp\deltafinkitxmlcodeinlinelatexdvp est une fonction qui renvoie 1 si kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp font partie de la même communauté et 0 sinon. La modularité peut être utilisée comme simple mesure de la qualité d'une partition, c'est-à-dire pour évaluer a posteriori une partition obtenue par une méthode quelconque. Cependant, la modularité peut aussi être utilisée comme méthode de partitionnement dans un algorithme qui cherche à la maximiser pour produire une partition cohérente. C'est sur ce principe que fonctionne l'algorithme utilisé, dit « méthode de Louvain » : il produit une partition du graphe à deux niveaux qui correspond à un optimum de modularité.

Le graphe est d'abord transformé en graphe non orienté, les arguments de la fonction (mode et edge.attr.comb) précisent que s'il y a un lien de kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp vers kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp et un lien de kitxmlcodeinlinelatexdvpjfinkitxmlcodeinlinelatexdvp vers kitxmlcodeinlinelatexdvpifinkitxmlcodeinlinelatexdvp, il faut les confondre et faire la somme des attributs des deux liens. Ainsi, si Créteil envoie 1000 individus vers Melun et Melun 500 individus vers Créteil, le sens et l'asymétrie de la relation seront perdus : on considérera qu'il y un seul lien non orienté entre ces deux communes représentant un flux de 1500 individus.

La fonction multilevel.community() renvoie une liste d'éléments qui contient les noms des sommets et leur appartenance aux communautés créées. On accède à ces éléments avec l'opérateur $ et on les regroupe dans un tableau.

undirGraph <- as.undirected(residGraph,
                            mode = "collapse",
                            edge.attr.comb = sum)

mltcomResid <- multilevel.community(
    undirGraph,
    weights = E(undirGraph) $NBFLUX
)

mltClust <- t(rbind(mltcomResid$memberships,
                    mltcomResid$names))

V(undirGraph) $CLUST <- mltClust[, 1]

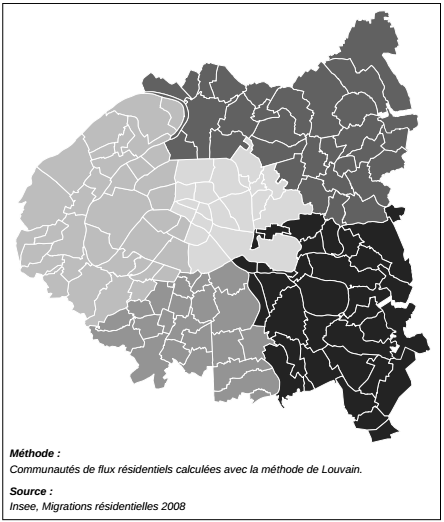
Là encore il sera intéressant de cartographier l'appartenance des communes à ces communautés avec les techniques présentées dans le Chapitre 10CHAPITRE 10 Introduction aux objets spatiaux et à la cartographie. Le résultat est affiché sur la carte suivante(25).

La fonction propose deux niveaux d'agrégation, c'est le plus agrégé qui est cartographié ici. Cinq sous-ensembles sont distingués qui correspondent presque exactement au découpage départemental. Seul le département 75 (Paris) est divisé en deux : les arrondissements de l'Ouest forment une communauté avec l'ensemble des communes des Hauts-de-Seine alors que les arrondissements de l'Est forment une communauté avec quelques communes limitrophes : Bagnolet, Montreuil ou Pantin.

Cette division Est-Ouest de Paris se retrouve dans bon nombre de variables sociales, économiques ou politiques, la plus fameuse étant la division du vote PS-UMP.

Visualiser les graphes est l'un des réflexes les plus courants, et peut-être l'un des plus trompeurs, en analyse de graphes. En effet, il faut être attentif aux paramètres de visualisation (épaisseur des liens, taille des nœuds) et aux principes de l'algorithme utilisé pour la visualisation. Les deux packages proposent des outils et options comparables. Le résultat par défaut est plus lisible avec statnet qu'avec igraph, mais les arguments des fonctions permettent d'obtenir des visualisations personnalisées de grande qualité, quel que soit le package utilisé.

La taille et la densité du graphe des mobilités résidentielles le rendent difficile à visualiser directement. Pour explorer sa structure, il faudrait travailler sur des sous-graphes, par exemple sur les communautés créées dans la section précédente, ou encore sur des sélections des liens. Il existe plusieurs façons de faire émerger des structures simples de graphes très denses, la plus simple étant de sélectionner pour chaque nœud le flux maximum envoyé.

Dans un premier temps, on récupère à partir de la matrice origine-destination l'index de colonne du flux maximum envoyé. Pour cela on applique la fonction which.max() ligne à ligne avec la fonction apply() (cf. Section 3.4L'application de fonctions sur des ensembles). Cette fonction renvoie un vecteur d'indexation : par exemple, si la première valeur de ce vecteur (correspondant à la commune 75101) est 11, ceci signifie que le flux maximum est atteint à la colonne 11 de la matrice. Il suffit ensuite d'utiliser cet index pour récupérer les noms de colonnes qui correspondent aux destinations des flux. La colonne 11 correspond par exemple à la commune 75111 : le flux résidentiel maximum en provenance du 1^er arrondissement se dirige vers le 11^e arrondissement. Ces liens sont réorganisés dans un tableau et la fonction graph.data.frame() transforme ce tableau en graphe.

indexMax <- apply(adjMat, 1, which.max)
destMax <- colnames(adjMat)[indexMax]
maxFlows <- data.frame(ORI = names(indexMax),
DES = destMax,
stringsAsFactors = FALSE)
maxGraph <- graph.data.frame(maxFlows, directed = TRUE)
maxGraph
## IGRAPH DN-- 143 143 --
## + attr: name (v/c)

Le graphe ainsi créé peut être visualisé directement avec la fonction générique plot(). La sortie par défaut n'est pas satisfaisante, il faut spécifier un certain nombre d'arguments graphiques pour obtenir un bon résultat, en particulier la couleur et l'épaisseur des liens (edge.color et edge.width), la couleur et la taille des nœuds (ici proportionnelle au degré), la disposition du graphe (layout). Un grand nombre d'arguments sont disponibles aussi bien dans igraph que dans statnet. Si l'utilisateur utilise beaucoup ces visualisations avec des réglages spécifiques, il peut facilement les encapsuler dans une fonction créée à cet effet et ainsi éviter de réécrire tous ces arguments à chaque fois.

plot(maxGraph,
     edge.color = "grey60",
     edge.width = 2,
     edge.curved = F,
     edge.arrow.mode = "-",
     vertex.frame.color = "white",
     vertex.color = "grey30",
     vertex.label = V(maxGraph) $name,
     vertex.label.cex = 0.8,
     vertex.label.color = "black",
     vertex.size = 2 * degree(maxGraph),
     layout = layout.fruchterman.reingold(maxGraph))

La sélection proposée dans cet exemple est rudimentaire, mais elle laisse déjà apparaître certaines structures : les grands arrondissements de l'Est parisien (11^e, 18^e, 19^e, 20^e) comme destination principale des flux intraparisiens; le 15^e arrondissement qui fait le lien entre les arrondissements de l'Ouest et les communes des Hauts-de-Seine (92); certains pôles d'attraction départementaux apparaissent, comme Saint-Denis (93066) pour le département de Seine-Saint-Denis (93) ou Créteil (94028) pour les communes du Val-de-Marne (94). Apparaissent également de petits sous-systèmes avec des communes peu nombreuses, souvent limitrophes, qui envoient leurs flux principaux les unes vers les autres, par exemple le trio Tremblay (93073)-Vaujours (93074)-Villepinte (93078).

L'argument layout prend comme argument le résultat d'algorithmes classiques de visualisation, comme celui de Fruchterman et Reingold ou celui de Kamada et Kawai. Ces algorithmes sont implémentés aussi bien dans igraph que dans statnet. Il est cependant possible pour l'utilisateur de proposer ses propres coordonnées sous forme d'une matrice de n lignes (nombre de nœuds) et 2 colonnes pour les coordonnées X et Y. En donnant comme argument les coordonnées géographiques des centroïdes des communes, il serait par exemple possible d'afficher le graphe dans le système de projection choisi.