Partie 6 Statistique bivariée▲
On entend par statistique bivariée l'étude des relations entre deux variables, celles-ci pouvant être quantitatives ou qualitatives.
Comme dans la partie précédente, on travaillera sur les jeux de données fournis avec l'extension rgrs et tirés de l'enquête Histoire de vie et du recensement 1999 :
2.
3.
R> data(hdv2003)
R> d <- hdv2003
R> data(rp99)
Deux variables quantitatives▲
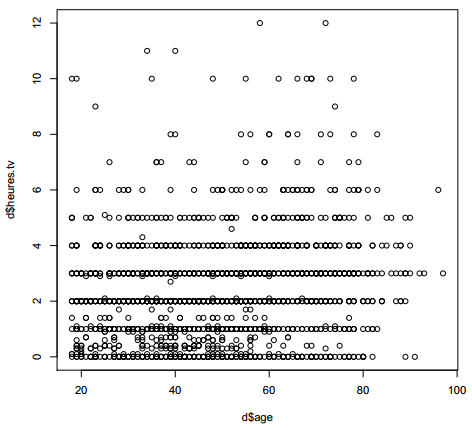
La comparaison de deux variables quantitatives se fait en premier lieu graphiquement, en représentant l'ensemble des couples de valeurs. On peut ainsi représenter les valeurs du nombre d'heures passées devant la télévision selon l'âge (figure 6.1).
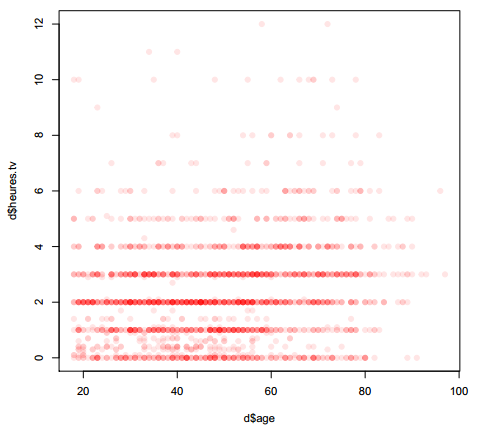
Le fait que des points sont superposés ne facilite pas la lecture du graphique. On peut utiliser une représentation avec des points semi-transparents (figure 6.2).
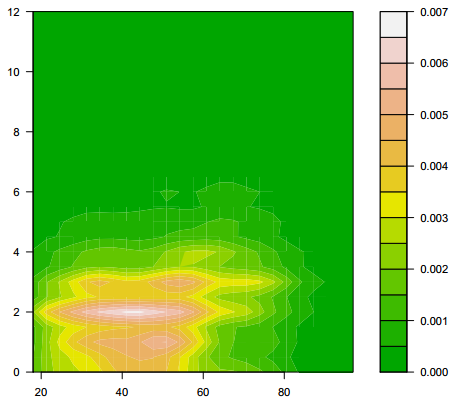
Plus sophistiqué, on peut faire une estimation locale de densité et représenter le résultat sous forme de « carte ». Pour cela on commence par isoler les deux variables, supprimer les observations ayant au moins une valeur manquante à l'aide de la fonction complete.cases, estimer la densité locale à l'aide de la fonction kde2d de l'extension MASS(21) et représenter le tout à l'aide d'une des fonctions image, contour ou filled.contour… Le résultat est donné figure 6.3.
Dans tous les cas, il n'y a pas de structure très nette qui semble se dégager. On peut tester ceci mathématiquement en calculant le coefficient de corrélation entre les deux variables à l'aide de la fonction cor :
R> cor(d$age, d$heures.tv, use = "complete.obs")
[1] 0.1776249L'option use permet d'éliminer les observations pour lesquelles l'une des deux valeurs est manquante. Le coefficient de corrélation est très faible.
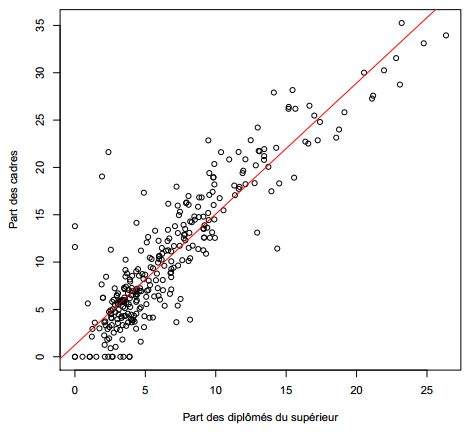
On va donc s'intéresser plutôt à deux variables présentes dans le jeu de données rp99, la part de diplômés du supérieur et la proportion de cadres dans les communes du Rhône en 1999.
R> plot(d$age, d$heures.tv)R> plot(d$age, d$heures.tv, pch = 19, col = rgb(1, 0, 0, 0.1))2.
3.
4.
R> library(MASS)
R> tmp <- d[, c("age", "heures.tv")]
R> tmp <- tmp[complete.cases(tmp), ]
R> filled.contour(kde2d(tmp$age, tmp$heures.tv), color = terrain.colors)
R> plot(rp99$dipl.sup, rp99$cadres, ylab = "Part des cadres",
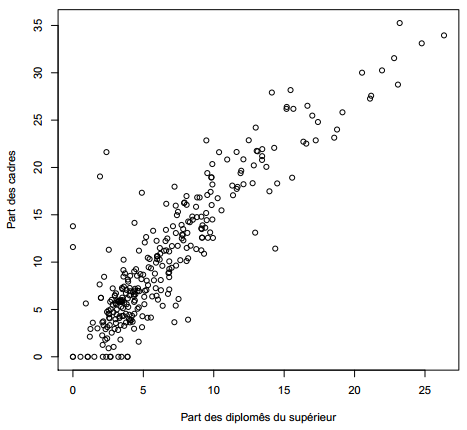
+ xlab = "Part des diplomés du supérieur")À nouveau, commençons par représenter les deux variables (figure 6.4 précédente). Ça ressemble déjà beaucoup plus à une relation de type linéaire.
Calculons le coefficient de corrélation :
R> cor(rp99$dipl.sup, rp99$cadres)
[1] 0.8975282C'est beaucoup plus proche de 1. On peut alors effectuer une régression linéaire complète en utilisant la fonction lm :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
R> reg <- lm(cadres ~ dipl.sup, data = rp99)
R> summary(reg)
Call:
lm(formula = cadres ~ dipl.sup, data = rp99)
Residuals:
Min 1Q Median 3Q Max
-9.6905 -1.9010 -0.1823 1.4913 17.0866
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.24088 0.32988 3.762 0.000203 ***
dipl.sup 1.38352 0.03931 35.196 < 2e-16 ***
---
Signif. codes: 0 ‘***' 0.001 ‘**' 0.01 ‘*' 0.05 ‘.' 0.1 ‘ ' 1
Residual standard error: 3.281 on 299 degrees of freedom
Multiple R-squared: 0.8056, Adjusted R-squared: 0.8049
F-statistic: 1239 on 1 and 299 DF, p-value: < 2.2e-16
Le résultat montre que les coefficients sont significativement différents de 0. La part de cadres augmente donc avec celle de diplômés du supérieur (ô surprise). On peut très facilement représenter la droite de régression à l'aide de la fonction abline (figure 6.5).
Une variable quantitative et une variable qualitative▲
Quand on parle de comparaison entre une variable quantitative et une variable qualitative, on veut en général savoir si la distribution des valeurs de la variable quantitative est la même selon les modalités de la variable qualitative. En clair : est-ce que l'âge de ceux qui écoutent du hard rock est différent de l'âge de ceux qui n'en écoutent pas ?
Là encore, l'idéal est de commencer par une représentation graphique. Les boîtes à moustaches sont parfaitement adaptées pour cela.
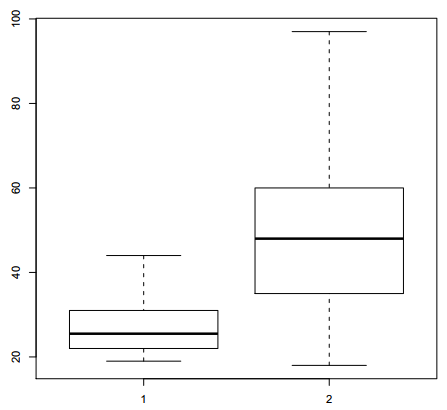
Si on a construit des sous-populations d'individus écoutant ou non du hard rock, on peut utiliser la fonction boxplot comme indiqué figure 6.6.
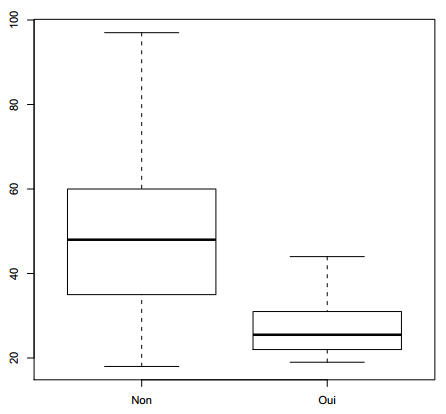
Mais construire les sous-populations n'est pas nécessaire. On peut utiliser directement la version de boxplot prenant une formule en argument (figure 6.7).
À première vue, ô surprise, la population écoutant du hard rock a l'air sensiblement plus jeune. Peut-on le tester mathématiquement ? On peut calculer la moyenne d'âge des deux groupes en utilisant la fonction tapply(22) :
2.
3.
R> plot(rp99$dipl.sup, rp99$cadres, ylab = "Part des cadres",
+ xlab = "Part des diplômés du supérieur")
R> abline(reg, col = "red")
2.
3.
R> d.hard <- subset(d, hard.rock == "Oui")
R> d.non.hard <- subset(d, hard.rock == "Non")
R> boxplot(d.hard$age, d.non.hard$age)
R> boxplot(age ~ hard.rock, data = d)
2.
3.
R> tapply(d$age, d$hard.rock, mean)
Non Oui
48.30211 27.57143
L'écart est très important. Est-il statistiquement significatif ? Pour cela on peut faire un test t de comparaison de moyennes à l'aide de la fonction t.test :
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
R> t.test(d$age ~ d$hard.rock)
Welch Two Sample t-test
data: d$age by d$hard.rock
t = 9.6404, df = 13.848, p-value = 1.611e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
16.11379 25.34758
sample estimates:
mean in group Non mean in group Oui
48.30211 27.57143
Le test est extrêmement significatif. L'intervalle de confiance à 95 % de la différence entre les deux moyennes, va de 14,5 ans à 21,8 ans.
Nous sommes cependant allés un peu vite en besogne, car nous avons négligé une hypothèse fondamentale du test t : les ensembles de valeur comparés doivent suivre approximativement une loi normale et être de même variance(23). Comment le vérifier ?
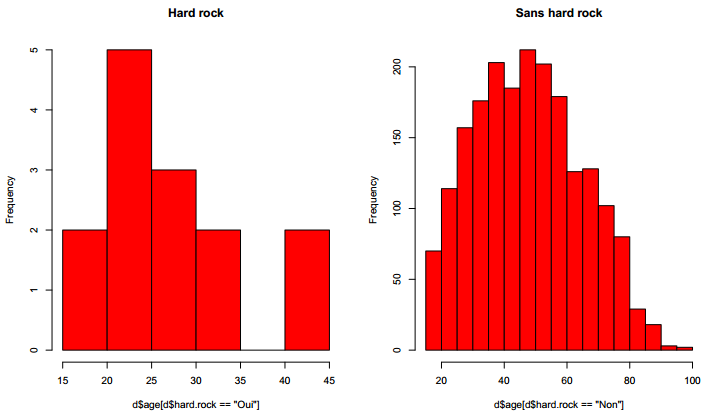
D'abord avec un petit graphique, comme sur la figure 6.8.
Ça a l'air à peu près bon pour les « Sans hard rock », mais un peu plus limite pour les fans de Metallica, dont les effectifs sont d'ailleurs assez faibles. Si on veut en avoir le cœur net on peut utiliser le test de normalité de Shapiro-Wilk avec la fonction shapiro.test :
2.
3.
4.
5.
6.
7.
8.
9.
10.
R> shapiro.test(d$age[d$hard.rock == "Oui"])
Shapiro-Wilk normality test
data: d$age[d$hard.rock == "Oui"]
W = 0.8693, p-value = 0.04104
R> shapiro.test(d$age[d$hard.rock == "Non"])
Shapiro-Wilk normality test
data: d$age[d$hard.rock == "Non"]
W = 0.9814, p-value = 2.084e-15
Visiblement, le test estime que les distributions ne sont pas suffisamment proches de la normalité dans les deux cas.
Et concernant l'égalité des variances ?
2.
3.
R> tapply(d$age, d$hard.rock, var)
Non Oui
285.62858 62.72527
L'écart n'a pas l'air négligeable. On peut le vérifier avec le test fourni par la fonction var.test :
2.
3.
R> par(mfrow = c(1, 2))
R> hist(d$age[d$hard.rock == "Oui"], main = "Hard rock", col = "red")
R> hist(d$age[d$hard.rock == "Non"], main = "Sans hard rock", col = "red")
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
R> var.test(d$age ~ d$hard.rock)
F test to compare two variances
data: d$age by d$hard.rock
F = 4.5536, num df = 1985, denom df = 13, p-value = 0.003217
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
1.751826 8.694405
sample estimates:
ratio of variances
4.553644
La différence est très significative. En toute rigueur le test t n'aurait donc pas pu être utilisé.
Damned ! Ces maudits tests statistiques vont-ils nous empêcher de faire connaître au monde entier notre fabuleuse découverte sur l'âge des fans de Sepultura ? Non ! Car voici qu'approche à l'horizon un nouveau test, connu sous le nom de Wilcoxon/Mann-Whitney. Celui-ci a l'avantage d'être non-paramétrique, c'est à dire de ne faire aucune hypothèse sur la distribution des échantillons comparés. Par contre, il ne compare pas des différences de moyennes, mais des différences de médianes :
2.
3.
4.
5.
6.
R> wilcox.test(d$age ~ d$hard.rock)
Wilcoxon rank sum test with continuity correction
data: d$age by d$hard.rock
W = 23980, p-value = 2.856e-06
alternative hypothesis: true location shift is not equal to 0
Ouf ! la différence est hautement significative(24). Nous allons donc pouvoir entamer la rédaction de notre article pour la Revue française de sociologie.
Deux variables qualitatives▲
La comparaison de deux variables qualitatives s'appelle en général un tableau croisé. C'est sans doute l'une des analyses les plus fréquentes lors du traitement d'enquêtes en sciences sociales.
Tableau croisé▲
La manière la plus simple d'obtenir un tableau croisé est d'utiliser la fonction table en lui donnant en paramètres les deux variables à croiser. En l'occurrence nous allons croiser un recodage du niveau de qualification regroupé avec le fait de pratiquer un sport.
On commence par calculer la variable recodée et par afficher le tri à plat des deux variables :
2.
3.
4.
5.
6.
7.
8.
9.
10.
R> d$qualreg <- as.character(d$qualif)
R> d$qualreg[d$qualif %in% c("Ouvrier specialise", "Ouvrier qualifie")] <- "Ouvrier"
R> d$qualreg[d$qualif %in% c("Profession intermediaire", "Technicien")] <- "Intermediaire"
R> d$qualreg <- factor(d$qualreg)
R> table(d$qualreg)
Autre Cadre Employe Intermediaire Ouvrier
58 260 594 246 495
R> table(d$sport)
Non Oui
1277 723
Le tableau croisé des deux variables s'obtient de la manière suivante :
2.
3.
4.
R> table(d$sport, d$qualreg)
Autre Cadre Employe Intermediaire Ouvrier
Non 38 117 401 127 381
Oui 20 143 193 119 114
On n'a cependant que les effectifs, ce qui rend difficiles les comparaisons. L'extension rgrs fournit des fonctions permettant de calculer les pourcentages lignes, colonnes et totaux d'un tableau croisé.
Les pourcentages lignes s'obtiennent avec la fonction lprop. Celle-ci s'applique au tableau croisé généré par table :
2.
3.
4.
5.
6.
R> tab <- table(d$sport, d$qualreg)
R> lprop(tab)
Autre Cadre Employe Intermediaire Ouvrier Total
Non 3.6 11.0 37.7 11.9 35.8 100.0
Oui 3.4 24.3 32.8 20.2 19.4 100.0
Ensemble 3.5 15.7 35.9 14.9 29.9 100.0
Les pourcentages ligne ne nous intéressent guère ici. On ne cherche pas à voir quelle est la proportion de cadres parmi ceux qui pratiquent un sport, mais plutôt quelle est la proportion de sportifs chez les cadres. Il nous faut donc des pourcentages colonnes, que l'on obtient avec la fonction cprop :
2.
3.
4.
5.
R> cprop(tab)
Autre Cadre Employe Intermediaire Ouvrier Ensemble
Non 65.5 45.0 67.5 51.6 77.0 64.4
Oui 34.5 55.0 32.5 48.4 23.0 35.6
Total 100.0 100.0 100.0 100.0 100.0 100.0
Dans l'ensemble, le pourcentage de personnes ayant pratiqué un sport est de 35,6 %. Mais cette proportion varie fortement d'une catégorie professionnelle à l'autre : 55,0 % chez les cadres contre 23,0 % chez les ouvriers.
À noter que l'on peut personnaliser l'affichage de ces tableaux de pourcentages à l'aide de différentes options, dont digits, qui règle le nombre de décimales à afficher, et percent, qui indique si on souhaite ou non rajouter un symbole % dans chaque case du tableau. Cette personnalisation peut se faire directement au moment de la génération du tableau, et dans ce cas elle sera utilisée par défaut :
2.
3.
4.
5.
6.
R> ctab <- cprop(tab, digits = 2, percent = TRUE)
R> ctab
Autre Cadre Employe Intermediaire Ouvrier Ensemble
Non 65.52% 45.00% 67.51% 51.63% 76.97% 64.37%
Oui 34.48% 55.00% 32.49% 48.37% 23.03% 35.63%
Total 100.00% 100.00% 100.00% 100.00% 100.00% 100.00%
ou bien ponctuellement en passant les mêmes arguments aux fonctions print (pour affichage dans R) ou copie (pour export vers un logiciel externe) :
2.
3.
4.
5.
6.
R> ctab <- cprop(tab)
R> print(ctab, percent = TRUE)
Autre Cadre Employe Intermediaire Ouvrier Ensemble
Non 65.5% 45.0% 67.5% 51.6% 77.0% 64.4%
Oui 34.5% 55.0% 32.5% 48.4% 23.0% 35.6%
Total 100.0% 100.0% 100.0% 100.0% 100.0% 100.0%
?2 et dérivés▲
Pour tester l'existence d'un lien entre les modalités des deux variables, on va utiliser le très classique test du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp(25). Celui-ci s'obtient grâce à la fonction chisq.test, appliquée au tableau croisé obtenu avec table(26) :
2.
3.
4.
5.
R> chisq.test(tab)
Pearson's Chi-squared test
data: tab
X-squared = 96.7983, df = 4, p-value < 2.2e-16
Le test est hautement significatif, on ne peut pas considérer qu'il y a indépendance entre les lignes et les colonnes du tableau.
On peut affiner l'interprétation du test en déterminant dans quelle case l'écart à l'indépendance est le plus significatif en utilisant les résidus du test. Ceux-ci sont notamment affichables avec la fonction residus de rgrs :
2.
3.
4.
R> residus(tab)
Autre Cadre Employe Intermediaire Ouvrier
Non 0.11 -3.89 0.95 -2.49 3.49
Oui -0.15 5.23 -1.28 3.35 -4.70
Les cases pour lesquelles l'écart à l'indépendance est significatif ont un résidu dont la valeur est supérieure à 2 ou inférieure à -2. Ici on constate que la pratique d'un sport est sur-représentée parmi les cadres et, à un niveau un peu moindre, parmi les professions intermédiaires, tandis qu'elle est sous-représentée chez les ouvriers.
Enfin, on peut calculer le coefficient de contingence de Cramer du tableau, qui peut nous permettre de le comparer par la suite à d'autres tableaux croisés. On peut pour cela utiliser la fonction cramer.vde rgrs :
2.
R> cramer.v(tab)
[1] 0.24199
Représentation graphique▲
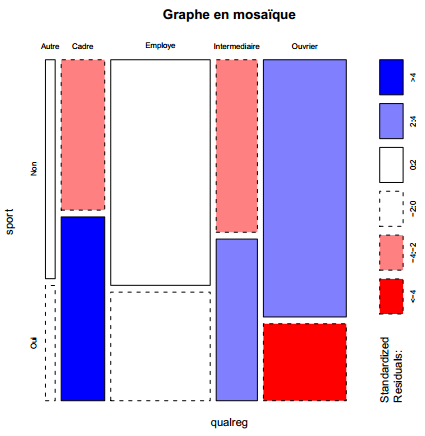
Enfin, on peut obtenir une représentation graphique synthétisant l'ensemble des résultats obtenus sous la forme d'un graphique en mosaïque, grâce à la fonction mosaicplot. Le résultat est indiqué figure 6.9.
Comment interpréter ce graphique haut en couleur(27) ? Chaque rectangle représente une case du tableau. Sa largeur correspond au pourcentage des modalités en colonnes (il y'a beaucoup d'employés et d'ouvriers et très peu d'« autres »). Sa hauteur correspond aux pourcentages-colonnes : la proportion de sportifs chez les cadres est plus élevée que chez les employés. Enfin, la couleur de la case correspond au résidu du test du kitxmlcodeinlinelatexdvp\chi^2finkitxmlcodeinlinelatexdvp correspondant : les cases en rouge sont sous-représentées, les cases en bleu surreprésentées, et les cases blanches sont statistiquement proches de l'hypothèse d'indépendance.
R> mosaicplot(qualreg ~ sport, data = d, shade = TRUE, main = "Graphe en mosaïque") R pour les sociologues (et assimilés)
R pour les sociologues (et assimilés)